A tegnap meghirdetett online kísérletünk jelentős érdeklődést vonzott: alig 12 óra alatt több mint ezer válasz érkezett, amiért minden résztvevőnek ezúton is köszönetet mondok. Az ezres szám már elegendő ahhoz, hogy az eredményekből statisztikát csináljunk. És persze eláruljuk a feladat megoldását is!

Mi is volt a kérdés? Egy asztalon négy kártyát látunk, kettőt felfelé, kettőt pedig lefelé fordítva. Tudható, hogy mindegyik kártya előlapján egy szám van, hátlapja pedig színes. A feladat az volt, hogy meg kellett mondani: mely kártyákat kell megfordítani ahhoz, hogy ellenőrizhessük, igaz-e a következő állítás: "A piros hátú kártyákon páros szám szerepel."

Emlékeztetőül álljon itt újra az ábra, s a könnyebbség végett jelöljük a kártyákat az A, B, C és D betűkkel:

A	B	C	D

És most lássuk, milyen válaszok érkeztek! Az első 1000 válasz feldolgozása alapján a válaszok megoszlása a következő:

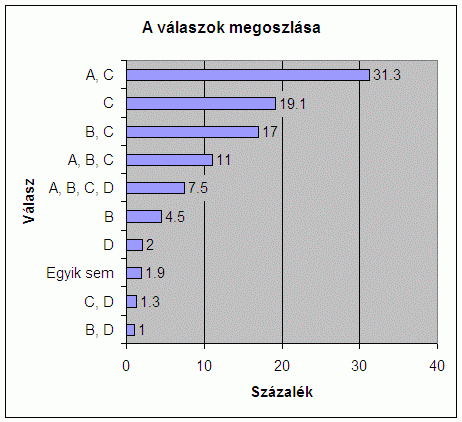
Örömhír, hogy a legtöbb válaszoló úgy vélte: az A és a C kártyákat kell megfordítani az állítás ellenőrzéséhez. Ez ugyanis a helyes válasz! Az örömbe azonban üröm is vegyül, ugyanis a válaszolók kevesebb mint egyharmada, pontosan 31,3%-a adta ezt a választ. A résztvevők 68,7%-a tehát hibásan válaszolt.

A második legnépszerűbb válasz (19,1%) szerint elegendő a C kártyát megfordítani, vagyis a piros hátút; a harmadik helyen pedig azok állnak (17%), akik a C mellett a B kártyát is megfordítanák, vagyis amin egy 8-as látható. Ezt követik azok (11%), akik szerint az első három kártyát mind meg kell fordítani. Hetvenöt válaszoló (azaz 7,5%-nyi) szerint biztos ami biztos, fordítsuk meg mind a négy kártyát. Tizenkilencen viszont egyetlen kártyát sem fordítanának meg, tíz válaszoló pedig a B és D kártyákat fordítaná meg, vagyis pontosan a helyes válasz ellentettjét adták.

Érdemes még megnézni azt is, hogy az egyes kártyák megfordítására a válaszolók mekkora része szavazott. Ezt az alábbi ábra mutatja:

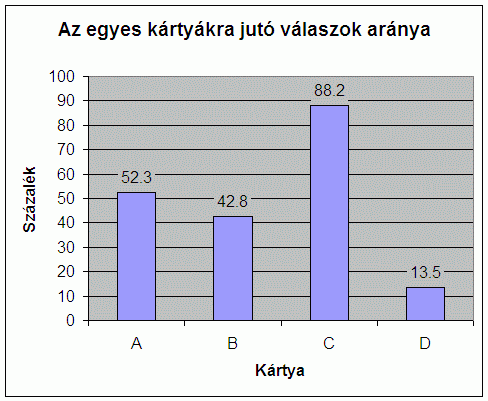
Magasan vezet (88,2%) a C kártya, vagyis a piros hátú - nagyon helyesen, hiszen ezt okvetlenül meg kell fordítanunk, elvégre látnunk kell, páros szám szerepel-e rajta. Az A kártyát, amelyen egy 3-as szerepel, viszont csak a válaszolók 52,3%-a fordítaná meg, a maradék 47,7% szerint ezt fölösleges megtenni - nekik sajnos nincs igazuk, hiszen ha ennek a kártyának a hátlapja netalántán piros, akkor az állítás máris nem lehet igaz! A válaszolók 42,8%-a szerint a B kártyát is meg kell fordítani - ők mind tévednek, hiszen igaz ugyan, hogy ezen egy 8-as látható, ami páros szám, de ez nekünk mindegy: akár piros a hátlapja, akár nem, a vizsgált állításról ez nem mond semmit. Az állítás ugyanis azt mondja, hogy ha egy kártya hátlapja piros, akkor azon páros számnak kell lennie - de nem mondja, hogy minden páros számot mutató kártya hátlapjának kötelező lenne pirosnak lenni; lehet az bármely más színű is. Végül pedig a válaszadók 13,5%-a szerint a kék hátú D kártyát is meg kell fordítani - holott ez teljesen fölösleges, hiszen az állítás a kék hátú kártyákkal egyáltalán nem foglalkozik.

Eddig tehát az eredmény, és a fentiekből talán már mindenki érti, miért is az "A és C" a jó válasz, és ha mást válaszolt, akkor már látja, miben is tévedett.

Rövidesen újabb, még izgalmasabb online kísérlet következik - talán már holnap! A messzemenőbb következtetések levonására pedig majd a második kísérlet kiértékelése után kerül sor - addig ne lőjük le a poént (s ezt kérném azoktól a kommentelőktől is, akik esetleg már sejtik, mire megy ki a játék).