 Már két hete, hogy meghirdettük második online kísérletünket, legfőbb ideje, hogy eláruljuk az eredményeket. Örömteli dolog, hogy várakozásainkhoz képest jóval több helyes megoldás érkezett.
Már két hete, hogy meghirdettük második online kísérletünket, legfőbb ideje, hogy eláruljuk az eredményeket. Örömteli dolog, hogy várakozásainkhoz képest jóval több helyes megoldás érkezett.E sorok írásakor az eddig beérkezett válaszok száma 807, de mivel 750-nél engedélyeztük a kommenteket és ez befolyásolhatta a további válaszokat, a kiértékelés az első 750 válasz alapján történt. Ezek közül is 33 nem volt értelmezhető, maradt tehát 717 érvényes válasz.
A feladat
Emlékeztetőül: a feladat az volt, hogy számhármasok tesztelésével fejtsünk meg egy bizonyos szabályt. Előre csak annyit mondtunk, hogy a (2,4,6) számhármas eleget tesz a szabálynak, ezután viszont a résztvevők tetszőleges számú számhármast ellenőrizhettek a weboldalba beágyazott űrlap segítségével, mely bármely számhármasra megmondta, az megfelel-e a szabálynak.
Először is leplezzük le a titkot, amely már egyébként is nyílt titok: a szabály mindössze az volt, hogy három különböző szám növekvő sorrendben szerepeljen.
Helyes és helytelen válaszok: statisztika
A helyes válaszok aránya: 55,2%
A beérkezett 717 érvényes válasz alapján ezt a szabályt a válaszolók 55,2%-a helyesen határozta meg! Őszintén szólva ennél gyengébb eredményre számítottunk. Érdemes persze megjegyezni, hogy a kísérlet első néhány órájában, amikor még az Index főoldalán is kint volt a kísérlet linkje, ennél valamivel gyengébb eredmény született: 47% volt a helyes válaszok aránya. Ez talán a kevésbé válogatott olvasóközönségnek tudható be (büszkék lennénk, ha rendszeres olvasóink jobban szerepelnének egy ilyen feladatban), de ez csak spekuláció, így a továbbiakban nem is foglalkozunk ezekkel a részeredményekkel.
A válaszolók 44,8%-a tehát hibás választ adott. Néhány esetben a válasz az volt, hogy bármilyen számhármas jó, a rendszer mindent elfogad, de a hibás válaszok túlnyomó többsége valamilyen, eléggé speciális szabályt adott meg, pl. "2-esével növekvő számok", "számtani sorozat", sőt, olyan megoldást is kaptunk, miszerint "az első szám adott, a második szám az első szám négyzete, a harmadik szám pedig az első szám köbe mínusz az első szám".
Megerősítések és cáfolatok
Kísérletünk célja azonban nem az volt, hogy megmutassuk, milyen sokan adnak téves választ, s ezen szörnyülködjünk. Sokkal inkább az érdekelt minket: mitől függ, hogy valaki helyes vagy helytelen megoldásra jut-e, ez ugyanis gondolkodásunk mechanizmusát világítja meg. Most már elárulhatjuk: amikor egy-egy résztvevő (nevezhetjük játékosnak is) elküldte nekünk válaszát, akkor két másik adatot is megkaptunk a válasszal együtt: azt, hogy a játékos hány esetben kapott "Megfelel", és hányban "Nem felel meg" választ, midőn számhármasokat ellenőrzött. Nevezzük a "Megfelel" válaszokat megerősítéseknek, a "Nem felel meg" válaszokat pedig cáfolatoknak.
Amikor valaki elkezdi a játékot, a kiinduló (2,4,6) számhármas alapján már van valamilyen elképzelése arról, milyen lehet a megtalálandó szabály, még ha mégoly bizonytalan is. Van tehát a fejében valamiféle feltevés, hipotézis. Amikor egy számhármast tesztel, ennek a hipotézisnek a helyességéről próbál meggyőződni: megerősítést vagy cáfolatot vár. A kapott visszajelzések alapján módosítja a hipotézist, majd azt is teszteli. Ez a folyamat tulajdonképpen elég jól modellezi a tudományos megismerés folyamatát.
Ebben a játékban két paraméter lehet fontos a folyamat végeredménye szempontjából:
- Hány számhármast tesztelünk?
- A tesztelések során milyen arányban kapunk cáfolatot, ill. megerősítést?
Egy játékos átlagosan 13,7 számhármast tesztelt.
Egy játékos az általa tesztelt számhármasoknak átlagosan 23,5%-ára kapott cáfolatot.
Egy játékos az általa tesztelt számhármasoknak átlagosan 23,5%-ára kapott cáfolatot.
Természetesen az, hogy valaki hány számhármast tesztel, azon is múlik, mennyire elszánt, ill. mennyire ér rá a feladattal bíbelődni. A játékosok átlagosan 13,7 számhármast teszteltek - persze előfordultak szélsőségek is: volt, aki beérte egyetlen próbával, de olyan is akadt, aki 267 számhármast ellenőrzött le. Figyelemre méltó viszont, hogy a teszteknek mindössze 23,5%-a zárult cáfolattal - ez azt jelenti, hogy a játékosok átlagosan több mint háromszor annyi megerősítést kaptak próbáikra, mint cáfolatot! Vajon befolyásolták-e ezek a paraméterek a megoldások helyességét?
Miben különböznek egymástól a helyesen és a helytelenül válaszolók?
Érdemes az említett két paramétert külön kiszámítani a helyes és a helytelen választ adók csoportjára:
| Helyesen válaszolók | Helytelenül válaszolók | |
| Tesztelt számhármasok átlagos száma | 20,6 | 5,3 |
| A cáfolt számhármasok átlagos részaránya | 35,6% | 8,6% |
Óriási különbségek figyelhetőek meg a két csoport között: míg a helyesen válaszolók átlagosan 20,6 számhármast teszteltek és ezek 35,6%-ára kaptak cáfolatot, a hibás választ adók megelégedtek átlagosan 5,3 számhármas tesztelésével, és ezeknek is mindössze 8,6%-ára kaptak cáfolatot. Ez persze csak úgy lehetséges, ha a játékosok jó része egyáltalán nem is kapott cáfolatot. Valóban: a hibás választ adók 70%-a úgy küldött be megoldást, hogy egyetlen számhármasra sem kapott "Nem felel meg" választ; ezzel szemben a helyesen válaszolóknak mindössze 1,2%-a jött rá a szabályra cáfoló visszajelzés nélkül.
Esély a helyes válaszra
Eddig azt vizsgáltuk, miben különbözik egymástól a helyes és a helytelen megoldást adók csoportja. Érdemes azonban a kérdést úgy is feltenni: mi a receptje a helyes válasz elérésének, azaz hogyan növelhetjük esélyünket arra, hogy helyes válaszra jussunk?
A fentiek alapján világos, hogy jó, ha minél több számhármast tesztelünk, és az is növeli az eredményességet, ha kellően magas arányban kapunk cáfoló visszajelzést tesztjeink során. Mivel az adatok szerint ez a két paraméter erősen összefügg egymással (azok, akik sok számhármast teszteltek, rendszerint nagyobb arányban is kaptak cáfolatokat), nehéz a hatásukat egymástól elkülöníteni. Az alaposabb elemzés azonban megmutatja, hogy a cáfolatok arányának van jelentősebb szerepe (ennek korrelációs együtthatója a válasz helyességével 0,69, míg a próbák számáé csak 0,48). Ez tehát azt jelenti, hogy a cáfoló visszajelzések arányának növelésével javíthatjuk leginkább az esélyünket arra, hogy egy efféle feladatnál eljussunk a helyes megoldáshoz.
Ezt illusztrálja az alábbi ábra is, amely azt mutatja, hogy a pontosan 7 számhármast tesztelők között hogyan függött a helyes választ adók aránya attól, hogy hány esetben kaptak cáfolatot:
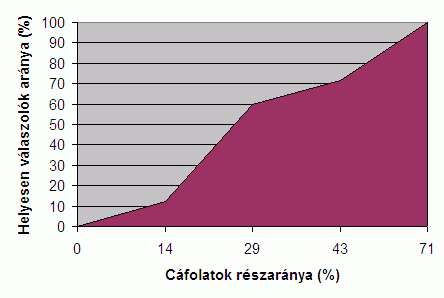
Mennyi cáfolatra van szükségünk a helyes válaszhoz?
Világos, hogy a helyes megoldáshoz való eljutás szempontjából mind a megerősített, mind a cáfolt próbák nélkülözhetetlenek. A megerősítések révén kiterjeszthetjük, a cáfolatok révén pedig szűkíthetjük a vizsgált hipotézis érvényességi körét. A cáfolatok optimális aránya attól is függ, hogy milyen típusú szabályokat vonunk be egyáltalán a hipotézistesztelés folyamatába, így erre konkrét számot nem lehet mondani. Az azonban sokatmondó, hogy a jelen feladat esetében az összes létező számhármasnak csupán mintegy 1/6-a felel meg a tényleges szabálynak.
A helyes válaszok sérülékenysége
Ehhez képest alacsonynak tűnik a helyes választ adók körében tapasztalt 35%-os cáfolatarány: ez azt jelenti, hogy még aki eljutott is a helyes megoldáshoz, az is átlagosan mintegy kétszer annyi megerősítő választ kapott próbálkozásai során, mint amennyi cáfolót. Ennek alapján könnyen lehet, hogy egy kicsit is bonyolultabb szabály már a most helyes megoldást adók nagy részén is kifogott volna. Vajon a helyes választ adók mekkora része tesztelt például negatív számokat? Ha a negatív számokra más szabály vonatkozott volna, alighanem jóval kisebb lenne a helyes megoldások aránya.
A megerősítési torzítás
Láthattuk tehát, hogy szinte mindenki, még a helyes választ adók is jóval több megerősítő visszajelzést kaptak próbáik során, mint amennyi cáfolót. Ez nem véletlen: ők maguk vitték be azokat a számhármasokat, amelyekre ezek a visszajelzések érkeztek, és hogy mikor álltak meg, azt egyedül ők határozták meg, tehát tetszőleges cáfolatarányt elérhettek volna. Azonban a résztvevők nagy többsége olyan módon vált eléggé biztossá a válaszában, hogy sok megerősítést kapott, kevés cáfolat mellett.
Ennek a jelenségnek a pszichológiában külön neve is van: megerősítési torzítás, az angol nyelvű szakirodalomban confirmation bias. Most már elárulhatjuk, hogy online kísérletünk voltaképpen Peter Cathcart Wason angol pszichológus 1960-ban publikált kísérletének reprodukálása volt, s a szakirodalomban "2-4-6 probléma" néven ismert. Ez az egyik alapkísérlet, mely a megerősítési torzítás létezését igazolja. Korábbi online kísérletünk (a piros hátú kártyákkal) szintén Wason találmánya, s Wason-féle szelekciós feladat néven ismert. Bár a szelekciós feladatnak más vonatkozásai is vannak, részben az arra adott hibás válaszok is a megerősítési torzítás következményei: azt a kártyalapot fordítjuk meg, amely igazolja a vizsgált állítást, s nem is jut eszünkbe megfordítani azt, amelyik cáfolhatná.
Állandóan a megerősítést keressük tehát, és irtózunk a cáfolatoktól. Emiatt pedig sok-sok tévhitet alakítunk ki magunkban, s ezekben ráadásul egyre biztosabbak leszünk. De ez már egy következő cikk témája lesz.
A bejegyzés trackback címe:
https://szkeptikus.blog.hu/api/trackback/id/tr53459352
Kommentek:
A hozzászólások a vonatkozó jogszabályok értelmében felhasználói tartalomnak minősülnek, értük a szolgáltatás technikai üzemeltetője semmilyen felelősséget nem vállal, azokat nem ellenőrzi. Kifogás esetén forduljon a blog szerkesztőjéhez. Részletek a Felhasználási feltételekben és az adatvédelmi tájékoztatóban.
D 2008.05.09. 16:00:06
"a korrelációs koefficiens 0,72."
A hipotézisem szerint /:)/ ezt a korrelációt mindenképp befolyásolja a következő két dolog:
- a feladat típusa (milyen bonyolult a szabály, mekkora valószínűséggel lehet pozitív/negatív példát találni)
- a résztvevő személy tapasztalata, prekoncepciója (pl egy számtani sorhoz hasonló példa alapján a tapasztalat miatt sokan ilyesmi formában keresik először a megoldást vagy egy írástudatlan ember valószínűleg formai hasonlóságok alapján állítana fel szabályt.)
A hipotézisem szerint /:)/ ezt a korrelációt mindenképp befolyásolja a következő két dolog:
- a feladat típusa (milyen bonyolult a szabály, mekkora valószínűséggel lehet pozitív/negatív példát találni)
- a résztvevő személy tapasztalata, prekoncepciója (pl egy számtani sorhoz hasonló példa alapján a tapasztalat miatt sokan ilyesmi formában keresik először a megoldást vagy egy írástudatlan ember valószínűleg formai hasonlóságok alapján állítana fel szabályt.)
wice 2008.05.09. 16:05:01
Andras: "azt írja a Wason-cikk, hogy az eliminatív/enumeratív index és a negatív válaszok aránya között rendkívül szignifikáns korreláció figyelhető meg, a korrelációs koefficiens 0,72."
csak az osszes tesztalany halmazara ertelmezve ennyi, mikozben van kulonbseg a vegul helyes valaszt adok es a rossz hipotezisnel megmaradok kozott? gyanitom, h igen.
nezd, az van, h neked meggyozodesed, h marpedig a magas pozitiv/negativ valaszarany egyertelmuen a bias kovetkezmenye. mi adtunk neked nem egy peldat arra, h hogyan billentheti pozitiv iranyba ezt az aranyt a keresett szabaly jellegebol es a kiindulopontbol eredo varhato logikus munkahipotezissorozat. te meg az egesz ellenvetest lenyegeben ujra es ujra azzal soprod le, h "marpedig ez a confirmation bias miatt van es kesz", ahelyett, h megmutatnad, miert nem torzithatjak a kezdeti feltetelek ebbe az iranyba az aranyt.
nem tul udito igy vitatkozni.
csak az osszes tesztalany halmazara ertelmezve ennyi, mikozben van kulonbseg a vegul helyes valaszt adok es a rossz hipotezisnel megmaradok kozott? gyanitom, h igen.
nezd, az van, h neked meggyozodesed, h marpedig a magas pozitiv/negativ valaszarany egyertelmuen a bias kovetkezmenye. mi adtunk neked nem egy peldat arra, h hogyan billentheti pozitiv iranyba ezt az aranyt a keresett szabaly jellegebol es a kiindulopontbol eredo varhato logikus munkahipotezissorozat. te meg az egesz ellenvetest lenyegeben ujra es ujra azzal soprod le, h "marpedig ez a confirmation bias miatt van es kesz", ahelyett, h megmutatnad, miert nem torzithatjak a kezdeti feltetelek ebbe az iranyba az aranyt.
nem tul udito igy vitatkozni.
hvuk 2008.05.09. 16:06:36
Igazából az a gond, hogy nem lehet matekkal normálisan megfogni a dolgot. Az pedig mindig gond.
Ha végtelen kísérletet végzünk, akkor valóban minden esetben amikor végtelen jó és végtelen rossz számhármas van, akkor az 50%-hoz konvergál. De sajnos ebből az égegyadta világon semmi nem következik véges esetre. Mondok két szabályt:
1. összes számhármas jó, amiben 100 ezernél kisebb számok szerepelnek (negatívak is).
2. a 2-4-6 jó, ezen kívül az összes számhármas ahol minden szám nagyobb 100 ezernél.
Teljesen biztos vagyok benne, hogy az első esetben a pozitív kísérletek száma kezdetben nagyon nagy lenne és onnan konvergálna lassan az 50% felé, míg a második esetben pont fordítva. Ha mondjuk egy szabályt akkor fogadunk el (ez rajtunk függ, de érdemes előre kikötni), ha 10-10 pozitív és negatív kísérlet is alátámasztja, akkor az első esetben a negatív kísérletek száma bőven 50% alatt lesz, míg a második esetben lényegesen felette. Nyilván azért, mert az első esetben egy nagy halom pozitív kimenetelű kisérletet végzünk el, amíg megtaláljuk a helyesnek vélt szabályt, míg a második esetben egy csomó negatív kimenetelűt és ezeket persze a végén nem egyenlíti ki a +10 kísérlet.
Kicsit ezt a végét még kifejtem. Tegyük fel, hogy ha a fenti első kísérletnél cáfoló (nem felel meg a valódi szabálynak) visszajelzést kapunk, akkor onnantól már egyből a jó szabályt - vagy legalábbis ahhoz közelállót) teszteljük, míg a 2. esetben ugyanaz egy nem cáfoló (azaz megfelel az igazi szabálynak) visszajelzés után következik be. Próbáljunk ki előtte mindkét esetben 20 számhármast mielőtt kitaláljuk a végső szabályt. Ekkor az első esetben 20 pozitív és 10 negatív kísérletet végeztünk (így áll elő a 10 negatív és a 10 pozitív kísérlet), azaz 33%-os lesz a negatív kísérletek száma. A 2. esetben viszont 20 negatív és 10 pozitív kimenetelű kísérletet hajtottunk végre, azaz itt a negatív kísérletek száma 66% volt. Pedig mindkettő 50%-hoz konvergált, csak az egyik alulról, a másik pedig felülről. De persze a konvergencia sebességében is lehet különbség.
Jogos a kérdésed, hogy vajon miért éppen 10 kísérletnél álltunk meg. Nos, miért ne? Végtelen lehetőség van, az összeset úgysem tudjuk tesztelni. Meg nem is fizetnek érte, így nem várható, hogy mondjuk 1000 számhármasig folytassuk. :)
Ha végtelen kísérletet végzünk, akkor valóban minden esetben amikor végtelen jó és végtelen rossz számhármas van, akkor az 50%-hoz konvergál. De sajnos ebből az égegyadta világon semmi nem következik véges esetre. Mondok két szabályt:
1. összes számhármas jó, amiben 100 ezernél kisebb számok szerepelnek (negatívak is).
2. a 2-4-6 jó, ezen kívül az összes számhármas ahol minden szám nagyobb 100 ezernél.
Teljesen biztos vagyok benne, hogy az első esetben a pozitív kísérletek száma kezdetben nagyon nagy lenne és onnan konvergálna lassan az 50% felé, míg a második esetben pont fordítva. Ha mondjuk egy szabályt akkor fogadunk el (ez rajtunk függ, de érdemes előre kikötni), ha 10-10 pozitív és negatív kísérlet is alátámasztja, akkor az első esetben a negatív kísérletek száma bőven 50% alatt lesz, míg a második esetben lényegesen felette. Nyilván azért, mert az első esetben egy nagy halom pozitív kimenetelű kisérletet végzünk el, amíg megtaláljuk a helyesnek vélt szabályt, míg a második esetben egy csomó negatív kimenetelűt és ezeket persze a végén nem egyenlíti ki a +10 kísérlet.
Kicsit ezt a végét még kifejtem. Tegyük fel, hogy ha a fenti első kísérletnél cáfoló (nem felel meg a valódi szabálynak) visszajelzést kapunk, akkor onnantól már egyből a jó szabályt - vagy legalábbis ahhoz közelállót) teszteljük, míg a 2. esetben ugyanaz egy nem cáfoló (azaz megfelel az igazi szabálynak) visszajelzés után következik be. Próbáljunk ki előtte mindkét esetben 20 számhármast mielőtt kitaláljuk a végső szabályt. Ekkor az első esetben 20 pozitív és 10 negatív kísérletet végeztünk (így áll elő a 10 negatív és a 10 pozitív kísérlet), azaz 33%-os lesz a negatív kísérletek száma. A 2. esetben viszont 20 negatív és 10 pozitív kimenetelű kísérletet hajtottunk végre, azaz itt a negatív kísérletek száma 66% volt. Pedig mindkettő 50%-hoz konvergált, csak az egyik alulról, a másik pedig felülről. De persze a konvergencia sebességében is lehet különbség.
Jogos a kérdésed, hogy vajon miért éppen 10 kísérletnél álltunk meg. Nos, miért ne? Végtelen lehetőség van, az összeset úgysem tudjuk tesztelni. Meg nem is fizetnek érte, így nem várható, hogy mondjuk 1000 számhármasig folytassuk. :)
hvuk 2008.05.09. 16:13:34
"És most jön a fontos felismerés: azt írja a Wason-cikk, hogy az eliminatív/enumeratív index és a negatív válaszok aránya között rendkívül szignifikáns korreláció figyelhető meg, a korrelációs koefficiens 0,72.
Ezt figyelembe véve megalapozottan állíthatjuk, hogy a pozitív/negatív torzítás a confirmation bias megbízható jele."
Ez tök jól hangzik, csak egy dolgot hagysz ki a számításból! Nem tudjuk, hogy vajon a 35% mekkora confirmation bias-t tartalmaz. Lehet, hogy egyáltalán nem szerepel benne (noha ez szerintem kizárt), de lehet, hogy tényleg jelentős a hatása. Azt kellene tudni, hogy vajon mekkora a confirmation bias nélküli érték várható értéke (nem a végtelenben, hanem a reálisan várható kísérletszámra, ami viszont erősen kísérleti személyfüggő).
A fenti Wason féle összefüggésből csak annyi következik, hogy a helytelenül megoldók 7% körüli cáfoló állítása a helyes megoldókhoz képest valóban a confirmation bias eredménye. De ebből nem következik, hogy a helyesen megoldóknál volt-e és hogy mekkora a confirmation bias hatása.
Ezt figyelembe véve megalapozottan állíthatjuk, hogy a pozitív/negatív torzítás a confirmation bias megbízható jele."
Ez tök jól hangzik, csak egy dolgot hagysz ki a számításból! Nem tudjuk, hogy vajon a 35% mekkora confirmation bias-t tartalmaz. Lehet, hogy egyáltalán nem szerepel benne (noha ez szerintem kizárt), de lehet, hogy tényleg jelentős a hatása. Azt kellene tudni, hogy vajon mekkora a confirmation bias nélküli érték várható értéke (nem a végtelenben, hanem a reálisan várható kísérletszámra, ami viszont erősen kísérleti személyfüggő).
A fenti Wason féle összefüggésből csak annyi következik, hogy a helytelenül megoldók 7% körüli cáfoló állítása a helyes megoldókhoz képest valóban a confirmation bias eredménye. De ebből nem következik, hogy a helyesen megoldóknál volt-e és hogy mekkora a confirmation bias hatása.
Szilágyi András 2008.05.09. 17:13:53
wice: ha van egy összefüggés, ami korreláció jellegű, akkor te azt az összefüggést nem tudod néhány olyan pont megmutatásával cáfolni, amely kilóg a várt tendenciából. Azért korreláció, mert vannak kilógó elemek benne. Ezért nem érdemes ellenpéldákkal előhozakodni. Persze, lehet gyártani olyan forgatókönyvet, hogy valaki mindig csak falszifikálni akar, és mégis mindig igen válaszokat kap. De nem ez a jellemző, az egész halmazt megnézve az a tendencia látszik, hogy az kap több nem választ, aki többször falszifikál. Gondolkodjatok el rajta, hogy miért áll fenn ez a korreláció.
hvuk: az, hogy a confirmation bias jelen van, az nem kérdés, csak a mértékét nem tudjuk megmondani. Attól, hogy valaki helyes megoldást adott, nem vált mágikusan biasmentes emberré. Egy teljesen folytonos átmenet van a hibás és a helyes választ adók között, a szétválasztás két csoportba mesterséges, kizárólag azon múlt, hogy én mit mondtam, hogy mi a helyes megoldás. Ha egy általánosabb szabályt mondok megoldásnak, a jelenlegi helyes megoldók nagy része helytelen megoldóvá válik.
hvuk: az, hogy a confirmation bias jelen van, az nem kérdés, csak a mértékét nem tudjuk megmondani. Attól, hogy valaki helyes megoldást adott, nem vált mágikusan biasmentes emberré. Egy teljesen folytonos átmenet van a hibás és a helyes választ adók között, a szétválasztás két csoportba mesterséges, kizárólag azon múlt, hogy én mit mondtam, hogy mi a helyes megoldás. Ha egy általánosabb szabályt mondok megoldásnak, a jelenlegi helyes megoldók nagy része helytelen megoldóvá válik.
wice 2008.05.09. 18:22:36
Andras: egyvalamire vagyok kivancsi: azoknal, akik Wason kiserleteben minden egyes munkahipotezisukre legalabb egy cafolo tesztet vegeztek, mekkora volt az ossz pozitiv/negativ valaszarany? mar ha ez kiderul a cikkbol. mert erzesem szerint naluk is joval magasabb volt 50/50 szazaleknal, a feladat jellegebol adodoan.
nyari mikulas (törölt) 2008.05.09. 18:35:40
Andras, sajnalom, hogy kotozkodesnek erzed amit irok, nem az volt a szandekom vele.
Hatarozott allaspontom, hogy tevedsz, es errol probaltalak ervekkel meggyozni.
Nem elso eset, hogy nem ertunk egyet, es egyszer sem tudtunk kozos nevezore jutni.
Nyilvan te ugy gondolod, hogy en tevedek es en nem vagyok hajlando a Te erveidet megfontolni, en meg forditva.
Igazad van, maradjunk ennyiben, remenytelen.
Orommel latom, hogy nem allok egyedul a velemenyemmel a kerdesben es hogy a tobbiekkel, akik ugyanazt mondjak, mint en, csak talan erthetobben, vagy kevesbe bantoan ervelnek, meg folytatod a vitat.
Ne hagyjatok abba, nagyon erdekes es tanulsagos!
Hatarozott allaspontom, hogy tevedsz, es errol probaltalak ervekkel meggyozni.
Nem elso eset, hogy nem ertunk egyet, es egyszer sem tudtunk kozos nevezore jutni.
Nyilvan te ugy gondolod, hogy en tevedek es en nem vagyok hajlando a Te erveidet megfontolni, en meg forditva.
Igazad van, maradjunk ennyiben, remenytelen.
Orommel latom, hogy nem allok egyedul a velemenyemmel a kerdesben es hogy a tobbiekkel, akik ugyanazt mondjak, mint en, csak talan erthetobben, vagy kevesbe bantoan ervelnek, meg folytatod a vitat.
Ne hagyjatok abba, nagyon erdekes es tanulsagos!
nyari mikulas (törölt) 2008.05.09. 19:54:45
Tegnap irtam, hogy elvegeztem ket kiserletet.
"Tudom, statisztikailag nem ertekelheto, de ezert leirom, mert erdekes, es azert is leirom, mert NEM tamogatja az en hipotezisemet.
Az elso kiserletben a blogon talalt peldat adtam fel egy amerikai egyetemistanak: 2,4,6.
14 probalkozasa volt, ebbol 8 helyes es 6 helytelen, mire azt mondta, hogy novekvo sorrend (negativ szamokra is tesztelte).
A masodik kiserletben ugyanennek a szemelynek a feladtam az 3,5,7 szamsor. 14 probalkozas (7 pozitiv es 7 negativ) utan feladta, nem talalja a szabalyt, ami az volt, hogy a szamok csak 1-gyel es onmagukkal oszthatoak.
En bevallom, arra szamitottam, hogy sokkal tobb helytelen probalkozast latok majd a masodik esetben. Nem igy tortent."
Ma megismeteltem a kiserletet egy masik egyetemistaval.
Az elso esetben(a 246 pleda) 8 helyes es 3 helytelen valaszt kapott, meghozza ilyen sorrendben:
++++++-+-+-
A masik esetben 8 negativ es egy pozitiv valaszt kapott
--------+
Ha talalok meg onkenteseket, akkor meg megismetlem majd, es kommentar (kotozkodes) nelkul beirom az eredmenyt.
Papiron vegeztuk a kiserletet, az alany leirt a harom szamot, en meg + vagy - jelet tettem melle.
"Tudom, statisztikailag nem ertekelheto, de ezert leirom, mert erdekes, es azert is leirom, mert NEM tamogatja az en hipotezisemet.
Az elso kiserletben a blogon talalt peldat adtam fel egy amerikai egyetemistanak: 2,4,6.
14 probalkozasa volt, ebbol 8 helyes es 6 helytelen, mire azt mondta, hogy novekvo sorrend (negativ szamokra is tesztelte).
A masodik kiserletben ugyanennek a szemelynek a feladtam az 3,5,7 szamsor. 14 probalkozas (7 pozitiv es 7 negativ) utan feladta, nem talalja a szabalyt, ami az volt, hogy a szamok csak 1-gyel es onmagukkal oszthatoak.
En bevallom, arra szamitottam, hogy sokkal tobb helytelen probalkozast latok majd a masodik esetben. Nem igy tortent."
Ma megismeteltem a kiserletet egy masik egyetemistaval.
Az elso esetben(a 246 pleda) 8 helyes es 3 helytelen valaszt kapott, meghozza ilyen sorrendben:
++++++-+-+-
A masik esetben 8 negativ es egy pozitiv valaszt kapott
--------+
Ha talalok meg onkenteseket, akkor meg megismetlem majd, es kommentar (kotozkodes) nelkul beirom az eredmenyt.
Papiron vegeztuk a kiserletet, az alany leirt a harom szamot, en meg + vagy - jelet tettem melle.
merenyi 2008.05.09. 20:44:33
tamas55,
valóban nem vagy egyedül a véleményeddel. én is megerősítenélek. emlékszem, hogy amikor játszottam a feladattal, engem határozottan bosszantott, hogy eleinte képtelen voltam negatív eredményt kapni, pedig az volt a célom. szinte minden értelmes kiinduló hipotézis a megoldás részhalmaza. ez a feladat egyszerűen úgy van megalkotva, hogy adják magukat a pozitív eredmények. csak akkor kaptam végre cáfolatot, amikor már rájöttem a megoldásra, és célirányosan azt teszteltem. az meg viszonylag gyorsan leellenőrizhető. nyilván jelen lehet a confirmation bias is a végeredményben, de alighanem elvész a feladat jellegéből adódó eltolódásban.
nekem még a korrelációs mentő érv is elég gyenge. az egész kísérlet nekem kicsit olyan volt, mintha valaki közölné velem, hogy illusztrálta (mégha informálisan is), hogy Magyarország időjárása esős - azzal a módszerrel, hogy a felhős napok száma meglepően nagy, mindezt úgy, hogy csak téli napokat néz. aztán felhozza mentő érvnek, hogy az eső erősen korrelál a felhős éggel.
valóban nem vagy egyedül a véleményeddel. én is megerősítenélek. emlékszem, hogy amikor játszottam a feladattal, engem határozottan bosszantott, hogy eleinte képtelen voltam negatív eredményt kapni, pedig az volt a célom. szinte minden értelmes kiinduló hipotézis a megoldás részhalmaza. ez a feladat egyszerűen úgy van megalkotva, hogy adják magukat a pozitív eredmények. csak akkor kaptam végre cáfolatot, amikor már rájöttem a megoldásra, és célirányosan azt teszteltem. az meg viszonylag gyorsan leellenőrizhető. nyilván jelen lehet a confirmation bias is a végeredményben, de alighanem elvész a feladat jellegéből adódó eltolódásban.
nekem még a korrelációs mentő érv is elég gyenge. az egész kísérlet nekem kicsit olyan volt, mintha valaki közölné velem, hogy illusztrálta (mégha informálisan is), hogy Magyarország időjárása esős - azzal a módszerrel, hogy a felhős napok száma meglepően nagy, mindezt úgy, hogy csak téli napokat néz. aztán felhozza mentő érvnek, hogy az eső erősen korrelál a felhős éggel.
Szilágyi András 2008.05.09. 20:59:48
wice: ez nem olvasható ki a cikkből, de nincs is jelentősége. Az, hogy valaki minden hipotézisét legalább egyszer megpróbálta cáfolni, nem jelenti azt, hogy nem próbálta sokkal többször megerősíteni őket, és az sem, hogy megismeréselméleti szempontból kifogástalanul cselekedett.
Egyébként meg úgy látom, hogy alapvetően olyasmikkel vitatkoztok, amiket én nem is állítok. Sőt, már azt sem tudom, mivel vitatkoztok tulajdonképpen. Szerintem minden világos, nem tudom, min lehet még itt vitatkozni.
Egyébként meg úgy látom, hogy alapvetően olyasmikkel vitatkoztok, amiket én nem is állítok. Sőt, már azt sem tudom, mivel vitatkoztok tulajdonképpen. Szerintem minden világos, nem tudom, min lehet még itt vitatkozni.
frank 2008.05.09. 23:11:11
Szerintem is minden vilagos, Andrasnak nincs igaza es az elemzese helytelen, a tobbieknek van igaza. Nem ertem miert kell csokonyosen kotni az ebet a karohoz.
Szilágyi András 2008.05.09. 23:14:33
Itt van még egy kis adalék:
szkeptikus.blog.hu/media/image/negarany.gif
Az ábra azt mutatja, hogyan függ a helyes megoldást adók aránya attól, hogy mekkora arányban kaptak negatív válaszokat a játékosok. A vízszintes tengely ábrázolja a negatív válaszok arányát, ez 0,05 szélességű tartományokra van osztva. A piros oszlopok azt mutatják, hogy az adott tartományba tartozó játékosoknak hány százaléka adott helyes megoldást. A kék vonal pedig azt mutatja, hány helyes megoldás tartozik az egyes tartományokba.
Ahogy várható volt, a helyes megoldáshoz való eljutás esélye növekszik a kapott negatív válaszok arányával. Magam sem gondoltam volna, de érdekes módon pont 0,5-nél maximális. Annak a 40 embernek, aki 45% és 50% közötti arányban kapott negatív válaszokat, 97,5%-a adott helyes megoldást, vagyis csak egy ember tévedett. A 35%-os válaszarány gyengébben teljesít ennél: 80 ember tartozik a 30%-35% tartományba, közülük 82,5% adott helyes megoldást, vagyis 14 ember tévedett.
Ez bizony alátámasztja azt, hogy az 50%-os negatív válaszarány jobb, mint a kisebb válaszarány. És azt is, hogy simán el lehet érni, 40 embernek sikerült.
szkeptikus.blog.hu/media/image/negarany.gif
Az ábra azt mutatja, hogyan függ a helyes megoldást adók aránya attól, hogy mekkora arányban kaptak negatív válaszokat a játékosok. A vízszintes tengely ábrázolja a negatív válaszok arányát, ez 0,05 szélességű tartományokra van osztva. A piros oszlopok azt mutatják, hogy az adott tartományba tartozó játékosoknak hány százaléka adott helyes megoldást. A kék vonal pedig azt mutatja, hány helyes megoldás tartozik az egyes tartományokba.
Ahogy várható volt, a helyes megoldáshoz való eljutás esélye növekszik a kapott negatív válaszok arányával. Magam sem gondoltam volna, de érdekes módon pont 0,5-nél maximális. Annak a 40 embernek, aki 45% és 50% közötti arányban kapott negatív válaszokat, 97,5%-a adott helyes megoldást, vagyis csak egy ember tévedett. A 35%-os válaszarány gyengébben teljesít ennél: 80 ember tartozik a 30%-35% tartományba, közülük 82,5% adott helyes megoldást, vagyis 14 ember tévedett.
Ez bizony alátámasztja azt, hogy az 50%-os negatív válaszarány jobb, mint a kisebb válaszarány. És azt is, hogy simán el lehet érni, 40 embernek sikerült.
Szilágyi András 2008.05.09. 23:25:52
És ezt akkor tovább is lehet gondolni. Ha elfogadjuk, hogy a megerősítési torzítástól mentes stratégia eredményezi a legnagyobb esélyt a helyes megoldás megtalálására, akkor a fenti ábra alapján arra következtethetünk, hogy az 50%-os negatív válaszarány felel leginkább meg a megerősítési torzítástól mentes gondolkodásnak. A 35%-os negatív válaszarány szuboptimális, ami arra utal, hogy mellette még megfigyelhető valamennyi megerősítési torzítás.
nyari mikulas (törölt) 2008.05.10. 04:32:36
Egy harmadik onkentest is talaltam a fentebb mar leirt osszehasonlitashoz.
a 2-6-6 (novekvo szamok) kiserlet eredmenye:
13+, 4-
++++--+++-+++++-+
ami meglepett, a 3-5-7 (primszamok) kiserlet:
5+, 1- igy
-+++++ helyes eredmeny
a 2-6-6 (novekvo szamok) kiserlet eredmenye:
13+, 4-
++++--+++-+++++-+
ami meglepett, a 3-5-7 (primszamok) kiserlet:
5+, 1- igy
-+++++ helyes eredmeny
hvuk 2008.05.10. 12:40:45
Na emberek, rájöttem, hogy hol van a confirmation bias elrejtve! Persze nem kicsit trükkös a dolog. Ott, hogy implicite felteszik a kísérletet végző személyek egy jó része, hogy a sorozat növekvő és a cáfolatként beadott számhármasok ennek a "láthatatlan" feltételnek általában megfelelnek. Ha emiatt az x, x+2, x+4 szabályt akarja valaki lecsekkolni, akkor ezt jó eséllyel egy növekvő sorozattal fogja megtenni. Nyilván, ha a cáfoló számhármast random módon választanánk ki a feltehető számhármasok köréből, akkor ez nem lépne fel. Persze akkor meg - András minden állításával ellentétben - 5/6 lenne a korrekt negatív válaszok száma és nem pedig 50%.
Más kérdés, hogy ez vajon a confirmation bias miatt van-e. Arra gondolok ugyanis, hogy _elvileg_ az egyetlen confirmation bias mentes stratégia az, hogy a számhármast véletlen módon választjuk ki úgy, hogy az negatív legyen a szabályra nézve, azonban mégsem hiszem azt, hogy bárki is ezt a stratégiát követné (és nem csak ebben a példában, hanem általában is mondjuk a tudományos kutatásban).
Igazából nagyon kíváncsi lennék egy olyan kísérletre, ahol nincs megadva egyetlen kiinduló számhármas sem! Azaz teljesen tiszta lappal kezdünk neki, kb. úgy mint ahogy az életnek is. Az szerintem jobban szimulálná a valódi gondolkodást és azt, hogy mitől alakul ki valakiben nagyon erős confirmation bias késztetés, míg másban miért nem.
Van még egy további dolog, amit még az eredeti topicban tettem szóvá, ez pedig a feladat leírásában a "szabály" szó kétértelműsége, amit a feladat kiírása sajnos egyáltalán nem oszlat el. Még egyszer vázolom az ott kifejtett problémát: a magyar (és persze az angolban is) nyelvben a szabály jelent algoritmust is, másrészt pedig jelent egyszerű feltételnek történő megfeleltetést is. Sőt, matematikai vonatkozásban szinte mindig az elsőt használjuk. Hozzáadódik ehhez az, hogy a feladat teljesen olyan típusúnak tűnt, hogy "itt van egy sorozat első három eleme és találd ki a negyediket", azzal a különbséggel, hogy itt nem a negyediket kellett megtalálni, hanem magát a szabályt.
Emiatt viszont nem lehet sajnos egyértelműen állítani, hogy a sorozat monoton voltának feltételezése confirmation bias lett volna. Annyira nem lehet, hogy szerintem nem is az volt. A helyes válaszadók 20 számhármast teszteltek döntésük meghozatala előtt, ha valaki a szabály szó algoritmus jelentéséből indult ki (szerintem a válaszolók nagyon döntő többsége így tett), akkor bizony legalább 4-5 olyan számhármast próbált ki, amely megfelelt az eredeti szabálynak. Ezután a hátralévő 15-16 próba már hiáűba volt confirmation bias mentes, te mégis csak 35-40% körüli negatív kísérletszámot mértél.
Van még egy következménye a szabály szó algoritmusként való értelmezésének. Ha olyan determinisztikus algoritmust keresek amelynek a 2,4,6 számhármas megfelel, akkor gyakorlatilag tetszőleges általam feltételezett algoritmus esetén nincs értelme mondjuk 8, 1, 153 sorozat tesztelésének, mivel nincs olyan értelmes algoritmus, amelynek mindkettő megfelel (megj.: nyilván van olyan algoritmus aminek mindkettő megfelel, de az olyan bonyolult, hogy nem fogom azt keresni egy ilyen feladatnál). Determinisztikus algoritmus esetén ugyanis éppen az a jó stratégia, ha először egy pozitív kísérletet végzek, azaz olyat ami megerősíti a szabályt. Egyszerűen így zárom ki hatékonyabban az általam kigondolt algoritmust (ennek oka triviális: determinisztikus algoritmus esetén egy véletlenszerűen kiválasztott számhármas nulla eséllyel fog megfelelni az igazi szabálynak, így egy negatív eredmény gyakorlatilag semmit nem mond az algoritmusomról). Ez tehát szerintem nem tekinthető confirmation bias-nak.
Én a feladat kiírásánál mindenképpen hangsúlyoztam volna, hogy itt nem algoritmusról van szó, hanem egyszerűen csak egy feltételről, hogy még a minimális esélyét is elkerüljem annak, hogy a feladat félreérthető legyen és így torz eredményt kapjak. András, Wason az eredeti kísérletében egész pontosan mit mondott az alanyoknak? Kiderül ez a leírásából? Mert szerintem ez egy nagyon komoly torzító tényező lehet!
Ui.: Lehet, hogy ez visszakozásnak tűnik a korábbi álláspontomhoz képest, pedig nem így van. Egyszerűen csak most tudtam lényegesen megfogalmazni azt, hogy miért volt a feladat kiírásának torzító hatása. Nem azért volt, mert implikálta a növekvő sorozatot, hanem azért, mert félreérthető módon algoritmust kezdtünk el keresni, amikor is egész más úton-módon indulunk el, mintha egy feltételt keresnénk (de persze ekkor fontos, hogy a számhármas mit implikál bennünk, azaz az milyen szóba jöhető algoritmusoknak felel meg).
Más kérdés, hogy ez vajon a confirmation bias miatt van-e. Arra gondolok ugyanis, hogy _elvileg_ az egyetlen confirmation bias mentes stratégia az, hogy a számhármast véletlen módon választjuk ki úgy, hogy az negatív legyen a szabályra nézve, azonban mégsem hiszem azt, hogy bárki is ezt a stratégiát követné (és nem csak ebben a példában, hanem általában is mondjuk a tudományos kutatásban).
Igazából nagyon kíváncsi lennék egy olyan kísérletre, ahol nincs megadva egyetlen kiinduló számhármas sem! Azaz teljesen tiszta lappal kezdünk neki, kb. úgy mint ahogy az életnek is. Az szerintem jobban szimulálná a valódi gondolkodást és azt, hogy mitől alakul ki valakiben nagyon erős confirmation bias késztetés, míg másban miért nem.
Van még egy további dolog, amit még az eredeti topicban tettem szóvá, ez pedig a feladat leírásában a "szabály" szó kétértelműsége, amit a feladat kiírása sajnos egyáltalán nem oszlat el. Még egyszer vázolom az ott kifejtett problémát: a magyar (és persze az angolban is) nyelvben a szabály jelent algoritmust is, másrészt pedig jelent egyszerű feltételnek történő megfeleltetést is. Sőt, matematikai vonatkozásban szinte mindig az elsőt használjuk. Hozzáadódik ehhez az, hogy a feladat teljesen olyan típusúnak tűnt, hogy "itt van egy sorozat első három eleme és találd ki a negyediket", azzal a különbséggel, hogy itt nem a negyediket kellett megtalálni, hanem magát a szabályt.
Emiatt viszont nem lehet sajnos egyértelműen állítani, hogy a sorozat monoton voltának feltételezése confirmation bias lett volna. Annyira nem lehet, hogy szerintem nem is az volt. A helyes válaszadók 20 számhármast teszteltek döntésük meghozatala előtt, ha valaki a szabály szó algoritmus jelentéséből indult ki (szerintem a válaszolók nagyon döntő többsége így tett), akkor bizony legalább 4-5 olyan számhármast próbált ki, amely megfelelt az eredeti szabálynak. Ezután a hátralévő 15-16 próba már hiáűba volt confirmation bias mentes, te mégis csak 35-40% körüli negatív kísérletszámot mértél.
Van még egy következménye a szabály szó algoritmusként való értelmezésének. Ha olyan determinisztikus algoritmust keresek amelynek a 2,4,6 számhármas megfelel, akkor gyakorlatilag tetszőleges általam feltételezett algoritmus esetén nincs értelme mondjuk 8, 1, 153 sorozat tesztelésének, mivel nincs olyan értelmes algoritmus, amelynek mindkettő megfelel (megj.: nyilván van olyan algoritmus aminek mindkettő megfelel, de az olyan bonyolult, hogy nem fogom azt keresni egy ilyen feladatnál). Determinisztikus algoritmus esetén ugyanis éppen az a jó stratégia, ha először egy pozitív kísérletet végzek, azaz olyat ami megerősíti a szabályt. Egyszerűen így zárom ki hatékonyabban az általam kigondolt algoritmust (ennek oka triviális: determinisztikus algoritmus esetén egy véletlenszerűen kiválasztott számhármas nulla eséllyel fog megfelelni az igazi szabálynak, így egy negatív eredmény gyakorlatilag semmit nem mond az algoritmusomról). Ez tehát szerintem nem tekinthető confirmation bias-nak.
Én a feladat kiírásánál mindenképpen hangsúlyoztam volna, hogy itt nem algoritmusról van szó, hanem egyszerűen csak egy feltételről, hogy még a minimális esélyét is elkerüljem annak, hogy a feladat félreérthető legyen és így torz eredményt kapjak. András, Wason az eredeti kísérletében egész pontosan mit mondott az alanyoknak? Kiderül ez a leírásából? Mert szerintem ez egy nagyon komoly torzító tényező lehet!
Ui.: Lehet, hogy ez visszakozásnak tűnik a korábbi álláspontomhoz képest, pedig nem így van. Egyszerűen csak most tudtam lényegesen megfogalmazni azt, hogy miért volt a feladat kiírásának torzító hatása. Nem azért volt, mert implikálta a növekvő sorozatot, hanem azért, mert félreérthető módon algoritmust kezdtünk el keresni, amikor is egész más úton-módon indulunk el, mintha egy feltételt keresnénk (de persze ekkor fontos, hogy a számhármas mit implikál bennünk, azaz az milyen szóba jöhető algoritmusoknak felel meg).
hvuk 2008.05.10. 12:42:24
"Persze akkor meg - András minden állításával ellentétben - 5/6 lenne a korrekt negatív válaszok száma és nem pedig 50%."
Helyesbítek: 5/6 lenne a negatív kísérletek száma amíg meg nem találjuk a végső szabályt (vagy egy ahhoz nagyon közeli szabályt), utánna természetesen konvergálna az 50%-hoz. Csak éppen felülről.
Helyesbítek: 5/6 lenne a negatív kísérletek száma amíg meg nem találjuk a végső szabályt (vagy egy ahhoz nagyon közeli szabályt), utánna természetesen konvergálna az 50%-hoz. Csak éppen felülről.
nyari mikulas (törölt) 2008.05.10. 14:03:06
(Andras, fordulj el egy pillanatra)
hvuk: elsore azt gondoltam, hogy a sorozat 2,4,6,... 8,10,12 lesz.
Teszteltem 8,10,12 szamokkal (ez pozitiv teszt). Utana teszteltem ugyanezt a hipotezist a 10,16, 26 szamokkal. (ez egy negativ teszt, mert nem felel meg a hipotezisemnek, ez cafolta volna a hipotezist!). A kiserletben megis pozitivkent lett ertekelve.
Ugyanakkor ha azt gondoltam volna eppen, hogy a szabaly Xn=X(n-1)+X(n-2), akkor az elso probamat kellett volna cafolo es masodikat megerosito kiserletnek tekinteni.
Azert nem lehet ezt a kiserletet igy ertekelni, mert nem tudja a kisertekelo, hogy en mit teszteltem eppen, es az, hogy egy teszt megerosito vagy cafolo, az nem a valasztol fugg, hanem az en kerdesemtol es az en varakozasomtol.
A masodik szemellyel vegzett masodik kiserletem, ahol eleinte csupa "-" valaszt kaptam nem azert volt "-" mert a valaszolo cafolni akarta a sajat felteveset. Az o szandeka megerosites lett volna, csak epp a nem a jo szabaly alapjan allitott elo szamokat, azert azok nem feleltek meg az en szabalyomnak.
A bias ott is megvolt! Csak a kiserlet igy nem azt merte.
hvuk: elsore azt gondoltam, hogy a sorozat 2,4,6,... 8,10,12 lesz.
Teszteltem 8,10,12 szamokkal (ez pozitiv teszt). Utana teszteltem ugyanezt a hipotezist a 10,16, 26 szamokkal. (ez egy negativ teszt, mert nem felel meg a hipotezisemnek, ez cafolta volna a hipotezist!). A kiserletben megis pozitivkent lett ertekelve.
Ugyanakkor ha azt gondoltam volna eppen, hogy a szabaly Xn=X(n-1)+X(n-2), akkor az elso probamat kellett volna cafolo es masodikat megerosito kiserletnek tekinteni.
Azert nem lehet ezt a kiserletet igy ertekelni, mert nem tudja a kisertekelo, hogy en mit teszteltem eppen, es az, hogy egy teszt megerosito vagy cafolo, az nem a valasztol fugg, hanem az en kerdesemtol es az en varakozasomtol.
A masodik szemellyel vegzett masodik kiserletem, ahol eleinte csupa "-" valaszt kaptam nem azert volt "-" mert a valaszolo cafolni akarta a sajat felteveset. Az o szandeka megerosites lett volna, csak epp a nem a jo szabaly alapjan allitott elo szamokat, azert azok nem feleltek meg az en szabalyomnak.
A bias ott is megvolt! Csak a kiserlet igy nem azt merte.
hvuk 2008.05.10. 14:15:42
Tamás (és András, ez neked is releváns)!
Mint megmutattam, nem ez a lényeg. Ha algoritmust tesztelsz és az a feltevésed, hogy az az x, x+2, x+4, x+6, ... alakú, akkor az 5, 10, 238 számhármas tesztelése nem minősíthető úgy, mintha az nem lenne confirmation bias. Mégpedig azért nem, mert egy determinisztikus algoritmust nem lehet ellenpéldákkal letesztelni (kivéve persze, ha véletlenül eltalálok egy, az igazi algoritmusnak megfelelő számhármast és _pozitív_ válasz jön ki). Szerintem egy teoretikus algoritmus tesztelésénél pont fordítva van: ott a confirmation bias igazából azt jelenti, ha nem megfelelő számhármast tesztelek, mivel ekkor van legnagyobb esélyem olyan visszajelzést kapnom, ami megerősít a hitemben, azaz így a legkisebb az esély a cáfolatra.
Mint megmutattam, nem ez a lényeg. Ha algoritmust tesztelsz és az a feltevésed, hogy az az x, x+2, x+4, x+6, ... alakú, akkor az 5, 10, 238 számhármas tesztelése nem minősíthető úgy, mintha az nem lenne confirmation bias. Mégpedig azért nem, mert egy determinisztikus algoritmust nem lehet ellenpéldákkal letesztelni (kivéve persze, ha véletlenül eltalálok egy, az igazi algoritmusnak megfelelő számhármast és _pozitív_ válasz jön ki). Szerintem egy teoretikus algoritmus tesztelésénél pont fordítva van: ott a confirmation bias igazából azt jelenti, ha nem megfelelő számhármast tesztelek, mivel ekkor van legnagyobb esélyem olyan visszajelzést kapnom, ami megerősít a hitemben, azaz így a legkisebb az esély a cáfolatra.
hvuk 2008.05.10. 14:30:02
Kicsit körüljárom egy példával! Tegyük fel, hogy az algoritmus a fenti x, x+2, x+4, x+6, ... és én is pont ezt tesztelem. Mondjuk összesen 20 tesztet végzek és már az elején a helyes algoritmust tesztelem. Nézzünk ekkor két szélsőséges tesztelési eljárást:
1. Úgy járok el, hogy _minden_ tesztben olyan számhármast tesztelek, ami nem x, x+2, x+4 alakú. Ekkor 20 negatív kimenetet kapok, amely kimenetek mindegyike megerősít a feltételezésemben. Azaz ez nagyon erős confirmation bias-nak tekinthető a 20 negatív kimenet ellenére is!
2. Mindig csak x, x+2, x+4 alakúakat tesztelek. Ekkor 20 pozitív választ kapok, amelyek mindegyike megerősíti a feltételezésemet, de ezek kísérletek mindegyikének nagyon nagy esélye van cáfolni az algoritmusomat, tehát nem igazán tekinthető jelentős confirmation bias-nak.
A 2. esetben azért van mégis confirmation bias, mert nem gondoltam azt végig, hogy így látszólag ugyan nagyon nagymértékben megerősítettem az algoritmusomat, de közben még más, szintén determinisztikus, de ennél bővebb szabályokat nem zártam. Mire gondolok? Konkrétan arra, hogy lehet az a definíció, hogy számtani sornak kell lennie, aminek az első két eleme határozza meg a különbséget. És én olyan algoritmust találtam ami d=2-re működik, de ezzel kizártam minden más d-t (például az 5-10-15 sorozatokat). Persze ha ez lenne a szabály, akkor kaphatnék pozitív kimenetet az első esetben, emiatt a példa nem tökéletes, de érzékelteti a problémát.
Persze ha nem algoritmust, hanem egy feltételt kell kitalálni - mint az eredeti feladatban - akkor ilyen gond nincs, de akkor persze tudatosítani kell, hogy itt nem algoritmusról van szó, különben torzul az eredmény.
1. Úgy járok el, hogy _minden_ tesztben olyan számhármast tesztelek, ami nem x, x+2, x+4 alakú. Ekkor 20 negatív kimenetet kapok, amely kimenetek mindegyike megerősít a feltételezésemben. Azaz ez nagyon erős confirmation bias-nak tekinthető a 20 negatív kimenet ellenére is!
2. Mindig csak x, x+2, x+4 alakúakat tesztelek. Ekkor 20 pozitív választ kapok, amelyek mindegyike megerősíti a feltételezésemet, de ezek kísérletek mindegyikének nagyon nagy esélye van cáfolni az algoritmusomat, tehát nem igazán tekinthető jelentős confirmation bias-nak.
A 2. esetben azért van mégis confirmation bias, mert nem gondoltam azt végig, hogy így látszólag ugyan nagyon nagymértékben megerősítettem az algoritmusomat, de közben még más, szintén determinisztikus, de ennél bővebb szabályokat nem zártam. Mire gondolok? Konkrétan arra, hogy lehet az a definíció, hogy számtani sornak kell lennie, aminek az első két eleme határozza meg a különbséget. És én olyan algoritmust találtam ami d=2-re működik, de ezzel kizártam minden más d-t (például az 5-10-15 sorozatokat). Persze ha ez lenne a szabály, akkor kaphatnék pozitív kimenetet az első esetben, emiatt a példa nem tökéletes, de érzékelteti a problémát.
Persze ha nem algoritmust, hanem egy feltételt kell kitalálni - mint az eredeti feladatban - akkor ilyen gond nincs, de akkor persze tudatosítani kell, hogy itt nem algoritmusról van szó, különben torzul az eredmény.
Szilágyi András 2008.05.10. 15:02:37
Inkább nézzétek meg a belinkelt ábrámat és ahhoz szóljatok hozzá!
Elgondolkodtatok-e, hogy miért van erős negatív korreláció a confirmation bias és a negatív válaszarány között?
Szerintem a következők miatt: Ahhoz, hogy eljussak egy megfelelően alátámasztott elmélethez (szabályhoz), ahhoz két dolgot kell tennem:
1. erre a szabályra kellően sok pozitív választ kell kapnom (enumeráció)
2. az alternatív szabályokra pedig negatív válaszokat kell kapnom, hogy ezeket kizárhassam (elimináció).
A confirmation bias azt jelenti, hogy elsősorban az enumerációt csinálom, az eliminációt pedig elhanyagolom. Fő oka az, hogy nem is gondolok alternatív szabályokra, nem törődöm vele, hogy azokat ki kéne zárni, vagy nem tartom ezt igazán fontosnak.
Aki confirmation bias nélkül jár el, az az enumerációra és eliminációra egyenlő súlyt helyez, és ezért nem érzi kellően biztosnak magát valamely szabály helyességében addig, amíg kellőképpen sok negatív választ nem kapott az alternatív szabályokra nézve.
Éppen ezért minél kevésbé bias-osabban jár el valaki, annál több negatív választ fog kapni. Emiatt van a korreláció.
Szépen látszik az ábrámból, hogy valóban növekszik a helyes megoldásra jutás esélye a negatív válaszok hányadának növekedésével. Emellett persze a helyes megoldást adók átlagosan több próbát is végeztek. Miért? Pont azért, mert nem nyugodtak meg addig, amíg az alternatív hipotézisekre elegendően sok negatív választ nem kaptak.
Ebben az értelemben pedig nem is volt annyira félrevezető a cikkben a megerősítés és a cáfolat szavakat használni a pozitív és a negatív válaszokra. A pozitív válasz a saját szabályom megerősítése, a negatív válasz pedig egy alternatív szabály cáfolata. A hipotézisem akkor válik erőssé, ha a saját szabályom kellően meg van erősítve, az alternatív szabályok pedig kellően meg vannak cáfolva, vagyis elegendően sokat kaptam mind pozitív, mind negatív válaszból.
Aki mondjuk csupa pozitív választ kapott, az hiába mondja, hogy de hát ezeket ő mind cáfolatként kapta, mert negatív választ várt a hipotézise alapján, valójában ezek a pozitív válaszok a végső szabályának megerősítéseivé váltak. És nem törődött azzal, hogy az alternatívákat pedig ki kéne zárni, amit viszont csak negatív válaszokkal lehet.
Elgondolkodtatok-e, hogy miért van erős negatív korreláció a confirmation bias és a negatív válaszarány között?
Szerintem a következők miatt: Ahhoz, hogy eljussak egy megfelelően alátámasztott elmélethez (szabályhoz), ahhoz két dolgot kell tennem:
1. erre a szabályra kellően sok pozitív választ kell kapnom (enumeráció)
2. az alternatív szabályokra pedig negatív válaszokat kell kapnom, hogy ezeket kizárhassam (elimináció).
A confirmation bias azt jelenti, hogy elsősorban az enumerációt csinálom, az eliminációt pedig elhanyagolom. Fő oka az, hogy nem is gondolok alternatív szabályokra, nem törődöm vele, hogy azokat ki kéne zárni, vagy nem tartom ezt igazán fontosnak.
Aki confirmation bias nélkül jár el, az az enumerációra és eliminációra egyenlő súlyt helyez, és ezért nem érzi kellően biztosnak magát valamely szabály helyességében addig, amíg kellőképpen sok negatív választ nem kapott az alternatív szabályokra nézve.
Éppen ezért minél kevésbé bias-osabban jár el valaki, annál több negatív választ fog kapni. Emiatt van a korreláció.
Szépen látszik az ábrámból, hogy valóban növekszik a helyes megoldásra jutás esélye a negatív válaszok hányadának növekedésével. Emellett persze a helyes megoldást adók átlagosan több próbát is végeztek. Miért? Pont azért, mert nem nyugodtak meg addig, amíg az alternatív hipotézisekre elegendően sok negatív választ nem kaptak.
Ebben az értelemben pedig nem is volt annyira félrevezető a cikkben a megerősítés és a cáfolat szavakat használni a pozitív és a negatív válaszokra. A pozitív válasz a saját szabályom megerősítése, a negatív válasz pedig egy alternatív szabály cáfolata. A hipotézisem akkor válik erőssé, ha a saját szabályom kellően meg van erősítve, az alternatív szabályok pedig kellően meg vannak cáfolva, vagyis elegendően sokat kaptam mind pozitív, mind negatív válaszból.
Aki mondjuk csupa pozitív választ kapott, az hiába mondja, hogy de hát ezeket ő mind cáfolatként kapta, mert negatív választ várt a hipotézise alapján, valójában ezek a pozitív válaszok a végső szabályának megerősítéseivé váltak. És nem törődött azzal, hogy az alternatívákat pedig ki kéne zárni, amit viszont csak negatív válaszokkal lehet.
hvuk 2008.05.10. 17:34:03
András!
A belinkelt ábrát megnéztem, de szerintem minimális az 50%-os és a 40%-os közötti különbség. Ebből szerintem egyáltalán nem következik, hogy az járt el helyesen, aki 50%-ban kapott pozitív és negatív választ.
Igazából ebben a hozzászólásodban csak ugyanazt szajkózod amit már eddig is mondtál. De eközben nem reagálsz sem a régebbi ellenérvekre, sem az újakra (lásd az én algoritmusra vonatkozó megjegyzéseimet). Tudnál ezekre is válaszolni!
Abban igazad van, hogy aki csak pozitív választ kapott, az valóban hiába hivatkozik erre. Viszont ő nem is fogja megtalálni a jó választ, tehát nem róla beszéltünk.
Viszont, hogy jó hírt is mondjak, rájöttem, hogy miről beszélsz. Te azt mondod, hogy a kísérletezőnek az összes kísérletet együtt kellene figyelembe venni és ezek alapján kellene az új kísérleti számhármast meghatároznia. Csakhogy az ember nem így működik, én például le sem írtam a régebbi példáimat. De nem az igazi gond, van ennél sokkal súlyosabb ellenérv is!
Ha a 2, 4, 6 számhármasból indulunk ki, akkor lényegesen több olyan egyszerű szabály képzelhető el (a 2 oldalas vagy matematikailag bonyolult szabályokat szerintem egyből mindenki kizárta), amely szigorúan növekedő számhármasokat generál, mint amely nem. Nyilván megszámolni nem tudjuk őket, de a lényeg az, hogy sokkal több ilyen szabály tudunk kitalálni, mint másfélét.
Ebből viszont az következik, hogy elvileg (nyilván most megfelelő hozzáállású embert véve alapul) azt relatíve kevés kísérlettel el lehet dönteni, hogy a sorozatnak növekvőnek kell lennie, azt azonban már nehezebb (értsd: több kísérlet kell hozzá), hogy rájöjjünk, hogy pontosan milyen szigorúan monoton szabály érvényes. Ez utóbbiaknál azonban csak és kizárólag szig. mon. számhármasokat lehet tesztelni, hiszen egy nem ilyen számhármas nem a felvetett szűkebb szabályt cáfolná, hanem csak az eredeti nagyon bő sigorúan növekvő felvetésünket.
Persze már írtam erről régebben is, de figyelmen kívül hagytad.
A belinkelt ábrát megnéztem, de szerintem minimális az 50%-os és a 40%-os közötti különbség. Ebből szerintem egyáltalán nem következik, hogy az járt el helyesen, aki 50%-ban kapott pozitív és negatív választ.
Igazából ebben a hozzászólásodban csak ugyanazt szajkózod amit már eddig is mondtál. De eközben nem reagálsz sem a régebbi ellenérvekre, sem az újakra (lásd az én algoritmusra vonatkozó megjegyzéseimet). Tudnál ezekre is válaszolni!
Abban igazad van, hogy aki csak pozitív választ kapott, az valóban hiába hivatkozik erre. Viszont ő nem is fogja megtalálni a jó választ, tehát nem róla beszéltünk.
Viszont, hogy jó hírt is mondjak, rájöttem, hogy miről beszélsz. Te azt mondod, hogy a kísérletezőnek az összes kísérletet együtt kellene figyelembe venni és ezek alapján kellene az új kísérleti számhármast meghatároznia. Csakhogy az ember nem így működik, én például le sem írtam a régebbi példáimat. De nem az igazi gond, van ennél sokkal súlyosabb ellenérv is!
Ha a 2, 4, 6 számhármasból indulunk ki, akkor lényegesen több olyan egyszerű szabály képzelhető el (a 2 oldalas vagy matematikailag bonyolult szabályokat szerintem egyből mindenki kizárta), amely szigorúan növekedő számhármasokat generál, mint amely nem. Nyilván megszámolni nem tudjuk őket, de a lényeg az, hogy sokkal több ilyen szabály tudunk kitalálni, mint másfélét.
Ebből viszont az következik, hogy elvileg (nyilván most megfelelő hozzáállású embert véve alapul) azt relatíve kevés kísérlettel el lehet dönteni, hogy a sorozatnak növekvőnek kell lennie, azt azonban már nehezebb (értsd: több kísérlet kell hozzá), hogy rájöjjünk, hogy pontosan milyen szigorúan monoton szabály érvényes. Ez utóbbiaknál azonban csak és kizárólag szig. mon. számhármasokat lehet tesztelni, hiszen egy nem ilyen számhármas nem a felvetett szűkebb szabályt cáfolná, hanem csak az eredeti nagyon bő sigorúan növekvő felvetésünket.
Persze már írtam erről régebben is, de figyelmen kívül hagytad.
Szilágyi András 2008.05.10. 17:45:25
Miféle ellenérvekre? Egyáltalán mivel vitatkozol te tulajdonképpen?
hvuk 2008.05.10. 17:50:13
Képzeletbeli alapos, de bias-tól egyáltalán nem mentes emberkénk így gondolkodhat.
1. koncepció: x, 2*x, 3*x. Teszteli mondjuk az 5, 10, 15 számhármassal, majd az 1, 2, 3-al. Figyelem, bias! :) Ezután kipróbálja a 0, 0, 0-t. Bias, de nem annak méred, nem baj, a végső szabályra nem az. Hümmögni kezd, kipróbálja a -1, -2, -3-at. Most sem jó. Gondol egy pozitív ellenpróbát (na végre, ez az első ilyen próbája!) 1, 4, 7 és pozitív választ kap! Elvégzett tehát 5 kísérletet, ebből 3 pozitív, 2 negatív.
2. koncepció: kis hümmögés után úgy gondolja, hogy lehet, hogy a nem szig. mon sorozatok mind rosszak. Teszteli az alapeseteket, meg 1-2 érdekes esetet, összesen mondjuk 15 kísérlet. Mind negatívnak méred.
3. -n. koncepció: Tesztel sok olyan számhármast ami az eddigi pozitív válaszokra illő szabályként megjelenhet. Alapos ember, akár 30 koncepciót is tesztelhet, amíg megállapítja, hogy bármely szigorúan növekvő számhármas jó. Ezen tesztek mind pozitívak, hiszen ezek csak és kizárólag szig. mon. növekvő számhármasokból álltak, hiszen ezeket a koncepciókat csak és kizárólag azokkal lehet tesztelni!
Összeségében végzett 50 kísérletet, amiből 17 lett negatív és 33 pozitív. Pedig pszichológia szempontból kizárólag az első 3 kísérlete volt confirmation bias-os, az összes többinél semmiféle ilyen nem játszott szerepet, végig nagyon önkritikus volt. Te azonban mégis jelentős confirmation bias-t tulajdonítanál neki. Meg tudnád mutatni, hogy az első 3 kísérleten kívül melyik kísérlet vol még szerinted pszichológiailag confirmation bias-os?
1. koncepció: x, 2*x, 3*x. Teszteli mondjuk az 5, 10, 15 számhármassal, majd az 1, 2, 3-al. Figyelem, bias! :) Ezután kipróbálja a 0, 0, 0-t. Bias, de nem annak méred, nem baj, a végső szabályra nem az. Hümmögni kezd, kipróbálja a -1, -2, -3-at. Most sem jó. Gondol egy pozitív ellenpróbát (na végre, ez az első ilyen próbája!) 1, 4, 7 és pozitív választ kap! Elvégzett tehát 5 kísérletet, ebből 3 pozitív, 2 negatív.
2. koncepció: kis hümmögés után úgy gondolja, hogy lehet, hogy a nem szig. mon sorozatok mind rosszak. Teszteli az alapeseteket, meg 1-2 érdekes esetet, összesen mondjuk 15 kísérlet. Mind negatívnak méred.
3. -n. koncepció: Tesztel sok olyan számhármast ami az eddigi pozitív válaszokra illő szabályként megjelenhet. Alapos ember, akár 30 koncepciót is tesztelhet, amíg megállapítja, hogy bármely szigorúan növekvő számhármas jó. Ezen tesztek mind pozitívak, hiszen ezek csak és kizárólag szig. mon. növekvő számhármasokból álltak, hiszen ezeket a koncepciókat csak és kizárólag azokkal lehet tesztelni!
Összeségében végzett 50 kísérletet, amiből 17 lett negatív és 33 pozitív. Pedig pszichológia szempontból kizárólag az első 3 kísérlete volt confirmation bias-os, az összes többinél semmiféle ilyen nem játszott szerepet, végig nagyon önkritikus volt. Te azonban mégis jelentős confirmation bias-t tulajdonítanál neki. Meg tudnád mutatni, hogy az első 3 kísérleten kívül melyik kísérlet vol még szerinted pszichológiailag confirmation bias-os?
hvuk 2008.05.10. 17:52:21
"Miféle ellenérvekre? Egyáltalán mivel vitatkozol te tulajdonképpen?"
Például azzal, hogy 50%-nak kellene lennie a várható negatív kísérletnek.
Azzal viszont nem vitatkozok, hogy a confirmation bias előfordulásában a helyes és a helytelen válaszolók között nagy volt a különbség és ez volt a döntő oka annak, hogy rossz választ adtak.
Például azzal, hogy 50%-nak kellene lennie a várható negatív kísérletnek.
Azzal viszont nem vitatkozok, hogy a confirmation bias előfordulásában a helyes és a helytelen válaszolók között nagy volt a különbség és ez volt a döntő oka annak, hogy rossz választ adtak.
nyari mikulas (törölt) 2008.05.10. 19:11:02
András, te totál reménytelen eset vagy.
nyari mikulas (törölt) 2008.05.10. 19:17:54
Andras:
-az abradon nem jelolted be, mekkora elteres szikgnifikans!
Jelentos-e az elteres a 0.35 hoz tartozo ~83% es a 0.5-hoz tartozo ~97% kozott? Ugye latod, hogy kevesebb eleme van a 0.5-os oszlopnap, igy a veletelen szoras is nagyobb lehet. Kiszamolod?
-figyelmen kivul hagytad (confirmation bias iskolapeldaja!) a 0.5 folotti eseteket, amikor is csokkent a helyes megoldasok aranya.
-Úgy látom, éles különbséget teszel a helytelen és a helyes választ adók között, mert a helytelen választ adók esetében elfogadod, hogy a confirmation bias a magyarázat, a helyes választ adók esetében viszont nem. De mi van, ha én most elárulom, hogy hazudtam, nem az volt a szabály, hogy növekvő számsort kell megadni, hanem azt, hogy vagy növekvő számsort kell megadni, vagy mínusz ezernél kisebb tetszőleges számokat? Minden adat marad a régi, és nem lesz senki, aki helyes megoldást adott volna.
-az abradon nem jelolted be, mekkora elteres szikgnifikans!
Jelentos-e az elteres a 0.35 hoz tartozo ~83% es a 0.5-hoz tartozo ~97% kozott? Ugye latod, hogy kevesebb eleme van a 0.5-os oszlopnap, igy a veletelen szoras is nagyobb lehet. Kiszamolod?
-figyelmen kivul hagytad (confirmation bias iskolapeldaja!) a 0.5 folotti eseteket, amikor is csokkent a helyes megoldasok aranya.
-Úgy látom, éles különbséget teszel a helytelen és a helyes választ adók között, mert a helytelen választ adók esetében elfogadod, hogy a confirmation bias a magyarázat, a helyes választ adók esetében viszont nem. De mi van, ha én most elárulom, hogy hazudtam, nem az volt a szabály, hogy növekvő számsort kell megadni, hanem azt, hogy vagy növekvő számsort kell megadni, vagy mínusz ezernél kisebb tetszőleges számokat? Minden adat marad a régi, és nem lesz senki, aki helyes megoldást adott volna.
vje 2008.05.10. 20:21:51
Örülök, hogy ilyen jó az arány... Azért nem reagáltam eddig, mert meg kellett várnom nyocévesemet, aki megtalálta a szbályt...
Megtalálta...
Biztosan a véletlen lehet -- számotokra, pedg ha nem is 13.valamennyi, de néhány próba alapján összejött. Nekem sem kellett 13...
Cca egy olyan gondolkodás, ami nem a "keretek" elvárások szerint működik, lazán néz egy ilyen feladatra... Az előzőre is..., ami -- ha jól értettem, elég gázos eredményt hozott...
Szép napot!
Megtalálta...
Biztosan a véletlen lehet -- számotokra, pedg ha nem is 13.valamennyi, de néhány próba alapján összejött. Nekem sem kellett 13...
Cca egy olyan gondolkodás, ami nem a "keretek" elvárások szerint működik, lazán néz egy ilyen feladatra... Az előzőre is..., ami -- ha jól értettem, elég gázos eredményt hozott...
Szép napot!
Szilágyi András 2008.05.10. 23:06:17
tamas,
a 35 és az 50% csoport között az eltérés szignifikáns, a mintaszámok ismeretében ezt ránézésre is tudni lehet, kiszámolva p=0.019.
Az 50% fölötti csökkenés beleillik az elméletbe, hiszen az már ellentétes irányú torzulás. Sajnos a mintaméret viszont 50% fölött rohamosan csökken, a további oszlopokat pedig már nem is tüntettem fel, mert ott már 5 körül van a mintaszám, így nagyon zajosak az adatok.
Pont az a számítás üzenete, hogy nincs éles különbség a helyes és a helytelen megoldók között, folytonos az átmenet közöttük. A negatívarány növekedésével egyre több ember éri el a helyes megoldást.
a 35 és az 50% csoport között az eltérés szignifikáns, a mintaszámok ismeretében ezt ránézésre is tudni lehet, kiszámolva p=0.019.
Az 50% fölötti csökkenés beleillik az elméletbe, hiszen az már ellentétes irányú torzulás. Sajnos a mintaméret viszont 50% fölött rohamosan csökken, a további oszlopokat pedig már nem is tüntettem fel, mert ott már 5 körül van a mintaszám, így nagyon zajosak az adatok.
Pont az a számítás üzenete, hogy nincs éles különbség a helyes és a helytelen megoldók között, folytonos az átmenet közöttük. A negatívarány növekedésével egyre több ember éri el a helyes megoldást.
Szilágyi András 2008.05.10. 23:17:58
hvuk,
meglehetősen extrém példa az 50 számhármassal próbálkozó ember. A 3-n koncepciókat kicsit elkented, a "tesztelés" közben honnét tudjuk, hogy mindig csak cáfolni akart? Sehonnan. Az alternatív szabályok 15 próbával való kizárása kicsit kevésnek tűnik ahhoz képest, hogy utána viszont 30 próbát szentelt a növekvő sorozatoknak. Ezzel együtt a magas próbaszám jó esélyt adott neki a helyes megoldásra, és a 34%-os negatívarány a grafikonom szerint már 82% fölötti esélyt jelent a helyes megoldáshoz való eljutásra, ami a magas próbaszámot is figyelembe véve még magasabb lehet. Az adataim szerint a 35% negatívarányúak között tipikusan olyanok jutnak téves megoldásra, akik 10-11 próbát tesznek, tehát 3-4 nem választ kapnak. Tehát arra lehet következtetni, hogy ennél az embernél elég alacsony lehetett a confirmation bias, megegyezően a te következtetéseddel. Hol a probléma?
Nem kéne elveszni az ilyen részletekben, a fő tendenciákat kell látni.
meglehetősen extrém példa az 50 számhármassal próbálkozó ember. A 3-n koncepciókat kicsit elkented, a "tesztelés" közben honnét tudjuk, hogy mindig csak cáfolni akart? Sehonnan. Az alternatív szabályok 15 próbával való kizárása kicsit kevésnek tűnik ahhoz képest, hogy utána viszont 30 próbát szentelt a növekvő sorozatoknak. Ezzel együtt a magas próbaszám jó esélyt adott neki a helyes megoldásra, és a 34%-os negatívarány a grafikonom szerint már 82% fölötti esélyt jelent a helyes megoldáshoz való eljutásra, ami a magas próbaszámot is figyelembe véve még magasabb lehet. Az adataim szerint a 35% negatívarányúak között tipikusan olyanok jutnak téves megoldásra, akik 10-11 próbát tesznek, tehát 3-4 nem választ kapnak. Tehát arra lehet következtetni, hogy ennél az embernél elég alacsony lehetett a confirmation bias, megegyezően a te következtetéseddel. Hol a probléma?
Nem kéne elveszni az ilyen részletekben, a fő tendenciákat kell látni.
bela2 2008.05.10. 23:18:11
Kedves Andras!
Csak hogy valaki a partodat is fogja - bar gondolom nincs szukseged ra...
Maximalisan igazad van, csak te elmeleti sikrol tekintesz a feladvanyra. Ellenlabasaid nem latnak ki a gyakorlati pelda mogul, azert nem ertik az ervelesed (pl. a fekete-feher mezoket). Sajnos ez a problema jellemzo altalanossagban is, nem tudunk elszakadni a foldhozragadt gondolkodastol, ami nem mindennapi "jozanparasztiesszel" felfoghato, az "fontoskodo tudomanyos hablaty". Az emberek nem vagynak az uj megismeresere, uj osszefuggesek felfedezesere, inkabb a vilag egyszerusitesere.
En csak biztatni tudlak, epp ezert van szukseg az ilyen blogokra!
Udv, bela
D 2008.05.10. 23:38:52
Kedves bela2!
Szerintem te ezt a vitát félreérted. Itt senki nem vitatja a confirmation bias létezésést. Az egyetlen, amit vitatunk, az a kísérlet eredményének értékelése.
És tökéletesen értjük a fekete-fehér mezős példát, de pont az a bajunk, hogy bizonyos szempontból rossz analógiának tartjuk. Azaz ez így nem igaz, hanem inkább egy olyan példának, aminél kicsi a torzítás - miközben megmutattuk, hogy tetszőleges irányú tetszőleges torzítást mutató feladatok is léteznek.
Szerintem te ezt a vitát félreérted. Itt senki nem vitatja a confirmation bias létezésést. Az egyetlen, amit vitatunk, az a kísérlet eredményének értékelése.
És tökéletesen értjük a fekete-fehér mezős példát, de pont az a bajunk, hogy bizonyos szempontból rossz analógiának tartjuk. Azaz ez így nem igaz, hanem inkább egy olyan példának, aminél kicsi a torzítás - miközben megmutattuk, hogy tetszőleges irányú tetszőleges torzítást mutató feladatok is léteznek.
nyari mikulas (törölt) 2008.05.10. 23:42:57
Andras, ezt kifejtened?
"Az 50% fölötti csökkenés beleillik az elméletbe, hiszen az már ellentétes irányú torzulás."
A blogban meg ezt irtad:
" a cáfoló visszajelzések arányának növelésével javíthatjuk leginkább az esélyünket arra, hogy egy efféle feladatnál eljussunk a helyes megoldáshoz."
A cafolatokbol nem latom, hogyan lehetne helytelen szabalyra kovetkeztetni?
Azzal egyetertek, hogy "Természetesen a ló túlsó oldalára sem kell átesni: ha csupa cáfoló visszajelzést kapunk hipotéziseinkre, akkor megintcsak nehezen tudjuk megtalálni a szabályt. "
A szabaly nem megtalalasa szerintem nem azonos a helytelen szabaly elfogadasaval.
Szoval ha valaki tobb mint 50%-ban cafolatot kap, az miert noveli az eselyet annak, hogy teves szabalyt allapitson meg?
"Az 50% fölötti csökkenés beleillik az elméletbe, hiszen az már ellentétes irányú torzulás."
A blogban meg ezt irtad:
" a cáfoló visszajelzések arányának növelésével javíthatjuk leginkább az esélyünket arra, hogy egy efféle feladatnál eljussunk a helyes megoldáshoz."
A cafolatokbol nem latom, hogyan lehetne helytelen szabalyra kovetkeztetni?
Azzal egyetertek, hogy "Természetesen a ló túlsó oldalára sem kell átesni: ha csupa cáfoló visszajelzést kapunk hipotéziseinkre, akkor megintcsak nehezen tudjuk megtalálni a szabályt. "
A szabaly nem megtalalasa szerintem nem azonos a helytelen szabaly elfogadasaval.
Szoval ha valaki tobb mint 50%-ban cafolatot kap, az miert noveli az eselyet annak, hogy teves szabalyt allapitson meg?
bela2 2008.05.10. 23:52:45
Eppen errol beszelek!
Nem ertitek a peldat. Ti kb. arrol beszeltek, hogy a felterkepezendo fekete terulet olyan nagy (=egyertelmu), hogy nem igazan lehet melletrafalni a probalkozassal. Ha meg mar jo sok fekete pontot talaltunk, a hatarokat nem is kell keresni. Az igazsag az, hogy barmekkora is (nagy vagy kicsi) a fekete terulet, korbe kell(ene) jarni!
Ti ugy erzitek, konnyu volt megtalalni a szabalyt. A tulnyomo tobbseg viszont nem megtalalta, hanem rahibazott.
Nem ertitek a peldat. Ti kb. arrol beszeltek, hogy a felterkepezendo fekete terulet olyan nagy (=egyertelmu), hogy nem igazan lehet melletrafalni a probalkozassal. Ha meg mar jo sok fekete pontot talaltunk, a hatarokat nem is kell keresni. Az igazsag az, hogy barmekkora is (nagy vagy kicsi) a fekete terulet, korbe kell(ene) jarni!
Ti ugy erzitek, konnyu volt megtalalni a szabalyt. A tulnyomo tobbseg viszont nem megtalalta, hanem rahibazott.
nyari mikulas (törölt) 2008.05.10. 23:53:42
Ha valaki masnak is trivialis, legyen olyan jo, es irjon par sort, mert nekem nem trivialis.
Hulye vagyok, de tanulni akarok.
Szoval ha valaki tobb mint 50%-ban cafolatot kap, az miert noveli az eselyet annak, hogy teves szabalyt allapitson meg?
Hulye vagyok, de tanulni akarok.
Szoval ha valaki tobb mint 50%-ban cafolatot kap, az miert noveli az eselyet annak, hogy teves szabalyt allapitson meg?
bela2 2008.05.11. 00:01:21
Tamas, a hatarfeluletek felterkepezesenel (altalanossagban) elhanyagolhato mennyisegu pontot kell tesztelnunk az alakzatok belsejeben. A hataron pedig egyenlo szamu fekete es feher pont van. Igy minel tobb pontra terjed ki a vizsgalat, annal kiegyenlitettebb kellene legyen az igaz/hamis arany. Termeszetesen egyedi peldakat, gondolatmenetet nehez statisztikai modszerekkel ertekelni, ezek inkabb trendek.
D 2008.05.11. 00:01:57
"Ti kb. arrol beszeltek, hogy a felterkepezendo fekete terulet olyan nagy (=egyertelmu), hogy nem igazan lehet melletrafalni a probalkozassal. Ha meg mar jo sok fekete pontot talaltunk, a hatarokat nem is kell keresni."
Nem, még csak hasonlóról sem. Arról beszélünk, hogy amennyiben nagyon kevés fekete pont van, azoknak a megtalálása közben nagyon sok fehéret fogunk kapni, viszont ha nagyon sok a fekete pont, akkor pedig fehérből keveset, és feketéből többet. Természetesen ha már megtaláltuk, hogy hol az átmenet, akkor a helyes stratégia szerint nyilván a megadottak szerint fogunk viselkedni, de az odáig eljutás befolyásolásával tetszőleges torzítást tudunk elérni.
Nem, még csak hasonlóról sem. Arról beszélünk, hogy amennyiben nagyon kevés fekete pont van, azoknak a megtalálása közben nagyon sok fehéret fogunk kapni, viszont ha nagyon sok a fekete pont, akkor pedig fehérből keveset, és feketéből többet. Természetesen ha már megtaláltuk, hogy hol az átmenet, akkor a helyes stratégia szerint nyilván a megadottak szerint fogunk viselkedni, de az odáig eljutás befolyásolásával tetszőleges torzítást tudunk elérni.
nyari mikulas (törölt) 2008.05.11. 00:03:00
Bela2,
nem allitotta senki, hogy konnyu volt megtalalni a szabalyt, egeszen masrol folyik a vita.
Van egy jelenseg: megerősítési torzítás, az angol nyelvű szakirodalomban confirmation bias.
Egyetertunk abban, hogy letezik.
Lexikon: Megerősítési torzítás az a tendencia, hogy ha egyszer egy nézetünket kinyilvánítottuk, minden ez után következő bizonyítékot a szerint ítélünk meg, hogy nézetünket amennyire csak lehetséges alátámassza.
ha angolul olvasol akkor ez talan jobb meghatarozas: "Confirmation bias refers to a type of selective thinking whereby one tends to notice and to look for what confirms one's beliefs, and to ignore, not look for, or undervalue the relevance of what contradicts one's beliefs."
Ebben az is benne van a fenti magyar meghatarozason tul, hogy nem keresunk olyan valaszt, ami varhatoan nem erositi meg a varakozasunkat.
Azt vitatjuk, hogy a fenti kiserlet ezt merte-e. Tobbunk szerint nem ezt merte.
nem allitotta senki, hogy konnyu volt megtalalni a szabalyt, egeszen masrol folyik a vita.
Van egy jelenseg: megerősítési torzítás, az angol nyelvű szakirodalomban confirmation bias.
Egyetertunk abban, hogy letezik.
Lexikon: Megerősítési torzítás az a tendencia, hogy ha egyszer egy nézetünket kinyilvánítottuk, minden ez után következő bizonyítékot a szerint ítélünk meg, hogy nézetünket amennyire csak lehetséges alátámassza.
ha angolul olvasol akkor ez talan jobb meghatarozas: "Confirmation bias refers to a type of selective thinking whereby one tends to notice and to look for what confirms one's beliefs, and to ignore, not look for, or undervalue the relevance of what contradicts one's beliefs."
Ebben az is benne van a fenti magyar meghatarozason tul, hogy nem keresunk olyan valaszt, ami varhatoan nem erositi meg a varakozasunkat.
Azt vitatjuk, hogy a fenti kiserlet ezt merte-e. Tobbunk szerint nem ezt merte.
nyari mikulas (törölt) 2008.05.11. 00:04:58
Bela2, kerlek ne ragadj le a terkepes peldanal, probald meg az eredeti szamos peldan kifejteni, "ha valaki tobb mint 50%-ban cafolatot kap, az miert noveli az eselyet annak, hogy teves szabalyt allapitson meg?"
bela2 2008.05.11. 00:06:28
A megerositesi torzitast merte a teszt. Es ti is ezt hangoztatjatok: Ha sok fekete pontot talaltunk es keves feheret, akkor nem kell koztuk megkeresni a hatart.
D 2008.05.11. 00:09:48
"Ha sok fekete pontot talaltunk es keves feheret, akkor nem kell koztuk megkeresni a hatart."
Mikor írt ilyet bárki? Mégegyszer elmondom: azon vitatkozunk, hogy a kísérletet befolyásolja, hogy a legelső fekete vagy legelső fehér pontot mennyi kísérlettel lehet megtalálni. Mert a határkeresés előtt legalább egy ellenkező színűt kell találni.
Mikor írt ilyet bárki? Mégegyszer elmondom: azon vitatkozunk, hogy a kísérletet befolyásolja, hogy a legelső fekete vagy legelső fehér pontot mennyi kísérlettel lehet megtalálni. Mert a határkeresés előtt legalább egy ellenkező színűt kell találni.
nyari mikulas (törölt) 2008.05.11. 00:11:12
"A megerositesi torzitast merte a teszt. Es ti is ezt hangoztatjatok: Ha sok fekete pontot talaltunk es keves feheret, akkor nem kell koztuk megkeresni a hatart. "
-A test szamokkal dolgozott, nem terkeppel.
-A hatar hol lenne mashol, mint a fekete es feher pontok kozott?
-A test szamokkal dolgozott, nem terkeppel.
-A hatar hol lenne mashol, mint a fekete es feher pontok kozott?
bela2 2008.05.11. 00:14:27
Megegyszer: a tartomanyok belsejeben veletlenul megtalalt fekete vagy feher pontok szama ELHANYAGOLHATO kellene legyen a hatarfeluleti pontok tesztelesehez kepest. Kerlek, probaljatok mar egy kicsit az ELMELETET megerteni! Nem arrol beszelunk, hogy 5 vagy 20 vagy akar 100 probalkozasbol mi az arany. Elmeletrol van szo!!! Es eppen ez a bias, hogy megelegedtek a belso pontokkal (meg itt is torzitva, amirol a ti vitatok szol) a hatarok keresese nelkul.
Szilágyi András 2008.05.11. 00:16:34
D: nem számít, hogy befolyásolja, nem a negatív válaszarány abszolút értékéből vonjuk le a következtetést, hanem a helyes és helytelen megoldók közötti különbségből. A kiinduló feltétel okozta torzítás mindkettőjüknél egyformán van jelen, viszont értelemszerűen a megerősítési torzítás a helytelen megoldóknál erősebb, mint a helyeseknél.
D 2008.05.11. 00:20:34
"Es eppen ez a bias, hogy megelegedtek a belso pontokkal (meg itt is torzitva, amirol a ti vitatok szol) a hatarok keresese nelkul."
Kérlek, értelmezd a szöveget, amit írunk. Senki nem azt mondta, hogy elégedjünk meg a példa szerinti belső pontokkal.
Kérlek, értelmezd a szöveget, amit írunk. Senki nem azt mondta, hogy elégedjünk meg a példa szerinti belső pontokkal.
D 2008.05.11. 00:27:28
"A kiinduló feltétel okozta torzítás mindkettőjüknél egyformán van jelen, viszont értelemszerűen a megerősítési torzítás a helytelen megoldóknál erősebb, mint a helyeseknél."
Ezzel egyetértek, de a helytelen megoldók pont a bias miatt kevesebb tesztet is végeznek, míg a helyes megoldókat az is zavarja, hogy túl sok pozitív megoldást kapnak. Ezért sok igenlő válasz mellett folyamatosan cáfolni akarnak, csak nem feltétlenül sikerül - de ez nem azt jelenti, hogy pozitív példát akarnak produkálni. Tehát a nagyon biasosokra szinte nem hat a torzítás, a kevéssé biasosokra viszont erősen.
Ezzel egyetértek, de a helytelen megoldók pont a bias miatt kevesebb tesztet is végeznek, míg a helyes megoldókat az is zavarja, hogy túl sok pozitív megoldást kapnak. Ezért sok igenlő válasz mellett folyamatosan cáfolni akarnak, csak nem feltétlenül sikerül - de ez nem azt jelenti, hogy pozitív példát akarnak produkálni. Tehát a nagyon biasosokra szinte nem hat a torzítás, a kevéssé biasosokra viszont erősen.
bela2 2008.05.11. 00:28:15
Nehez esetek vagytok!
A sajat VELETLENUL megtalalt belso pontjaitokkal vagytok megelegedve. Ti azt ertelmezitek bias-nak, hogy a VELETLENUL megtalalt jo es rossz pontok hogy aranylanak egymashoz. Pedig arrol van szo, hogy a tenylegesen kiegyenlito hatasu hatarkeresest meg sem teszitek. Ezt probaljatok mar megerteni, hogy tokeletesen mindegy kellene legyen, milyen meretu es elhelyezkedesu a fekete es feher terulet, a hatart mindenkeppen VEGTELEN szamu probalkozassal lehet csak megtalalni, aminek kb. fele-fele feher es fekete. Ennek egy valodi tesztpelda megoldasa nyilvan csak egy kisebb-nagyobb vetulete. Nem tokeletes, de legalabb lehet rajta merni.
A sajat VELETLENUL megtalalt belso pontjaitokkal vagytok megelegedve. Ti azt ertelmezitek bias-nak, hogy a VELETLENUL megtalalt jo es rossz pontok hogy aranylanak egymashoz. Pedig arrol van szo, hogy a tenylegesen kiegyenlito hatasu hatarkeresest meg sem teszitek. Ezt probaljatok mar megerteni, hogy tokeletesen mindegy kellene legyen, milyen meretu es elhelyezkedesu a fekete es feher terulet, a hatart mindenkeppen VEGTELEN szamu probalkozassal lehet csak megtalalni, aminek kb. fele-fele feher es fekete. Ennek egy valodi tesztpelda megoldasa nyilvan csak egy kisebb-nagyobb vetulete. Nem tokeletes, de legalabb lehet rajta merni.
Szilágyi András 2008.05.11. 00:30:07
Közben olvasgattam egy kis szakirodalmat. Érdekes, hogy egy Wetherick nevű fickó 1962-ban hasonló érvekkel kritizálta Wason kísérletét, mint ti, azaz hogy nem lehet tudni, ki mikor szánta megerősítésnek vagy cáfolatnak a próbáját. Wason erre további elemzésekkel és újabb kísérletekkel válaszolt, megerősítve korábbi következtetéseit. Megmutatta, hogy sok ember nemhogy nem alkalmazza a falszifikációt, de még a fogalmat sem érti.
D 2008.05.11. 00:38:33
"A sajat VELETLENUL megtalalt belso pontjaitokkal vagytok megelegedve."
Nem. Ugyanis adott a kiinduló kezdőpont, ami itt a kezdeti számhármasnak felel meg.
Határértékben (végtelen pont) természetesen igazad van. De mi arról beszélünk, hogy egy emberekkel végzett kísérletben nem lesz végtelen teszt, és adott esetben a lassú konvergencia miatt adódhat torzítás.
Nem. Ugyanis adott a kiinduló kezdőpont, ami itt a kezdeti számhármasnak felel meg.
Határértékben (végtelen pont) természetesen igazad van. De mi arról beszélünk, hogy egy emberekkel végzett kísérletben nem lesz végtelen teszt, és adott esetben a lassú konvergencia miatt adódhat torzítás.
Szilágyi András 2008.05.11. 00:38:34
"Tehát a nagyon biasosokra szinte nem hat a torzítás, a kevéssé biasosokra viszont erősen."
Ez eléggé spekulatív megállapítás. De mindegy is, mert ennek ellenére látjuk a kisebb biast a helyes megoldóknál a negatívarányban is és a próbaszámban is.
Egyre inkább az az érzésem, hogy az motivál benneteket, hogy nektek is kevés negatív próbátok volt, és meg vagytok sértődve, hogy valaki azt mondja, hogy nálatok is lehetett bias. Még mit nem! A feladat volt rossz! Na persze.
Ez eléggé spekulatív megállapítás. De mindegy is, mert ennek ellenére látjuk a kisebb biast a helyes megoldóknál a negatívarányban is és a próbaszámban is.
Egyre inkább az az érzésem, hogy az motivál benneteket, hogy nektek is kevés negatív próbátok volt, és meg vagytok sértődve, hogy valaki azt mondja, hogy nálatok is lehetett bias. Még mit nem! A feladat volt rossz! Na persze.
bela2 2008.05.11. 00:41:57
A kiindulopont 1 pont. Vesd ossze a vegtelennel. Vagy maradjunk a foldon :-) es vesd ossze a nagyon sokkal.
bela2 2008.05.11. 00:50:52
Andras, rokonlelkek vagyunk. En is valamifele furcsan ertelmezett presztizsfeltest erzek. Kicsit hasonlo a helyzet a kartyas teszt utanival, bar most itt szerencsere sokkal magasabb szintu a vita. Mindenesetre a magyar nem hibazhat, esetleg csobe huzhatjak vagy hibas kovetkeztetest vonhatnak le rola. Pedig ez nem arrol szol, hogy hulye aki nem hozta ki az 50%-ot, egyszeruen csak ilyenek vagyunk.
nyari mikulas (törölt) 2008.05.11. 01:16:23
Andras, nagyon olcso dolog, a vitapartner szemelyet tamadni.
Altalaban ez azt mutatja, hogy valaki kifogyott az ervekbol.
Argumentum ad hominem, ha ismered a fogalmat. Ha nem, akkor en.wikipedia.org/wiki/Ad_hominem
Mellesleg tevedsz, elegendoen sok negativ visszajelzesem volt, nagy szamokra, negativ szamokra is teszteltem. Sajnalatos, hogy nem orizted meg IP szerint a valaszokat.
A kiserlet valoban jol szemlelteti a megerositesi torzitast.
Abban nem ertunk egyet, hogy a negativ valaszok aranya meroszama lehetne a torzitasnak.
Abban sem ertunk egyet, hogy ebben a konkret kiserletben eppen 50% lett volna a torzitas nelkuli legmegbizhatobban helyes eredmenyt ado strategia.
Erre megprobalhatsz ervelni, ha az ervedet nem ertjuk, akkor megprobalhatod mashogy megkozelitve kifejteni az allaspontodat.
Vagy sertodotten lezarod a vitat azzal, hogy neked van igazad, mi ostoba kotozkodok vagyunk.
Altalaban ez azt mutatja, hogy valaki kifogyott az ervekbol.
Argumentum ad hominem, ha ismered a fogalmat. Ha nem, akkor en.wikipedia.org/wiki/Ad_hominem
Mellesleg tevedsz, elegendoen sok negativ visszajelzesem volt, nagy szamokra, negativ szamokra is teszteltem. Sajnalatos, hogy nem orizted meg IP szerint a valaszokat.
A kiserlet valoban jol szemlelteti a megerositesi torzitast.
Abban nem ertunk egyet, hogy a negativ valaszok aranya meroszama lehetne a torzitasnak.
Abban sem ertunk egyet, hogy ebben a konkret kiserletben eppen 50% lett volna a torzitas nelkuli legmegbizhatobban helyes eredmenyt ado strategia.
Erre megprobalhatsz ervelni, ha az ervedet nem ertjuk, akkor megprobalhatod mashogy megkozelitve kifejteni az allaspontodat.
Vagy sertodotten lezarod a vitat azzal, hogy neked van igazad, mi ostoba kotozkodok vagyunk.
frank 2008.05.11. 01:23:37
"A kiindulopont 1 pont. Vesd ossze a vegtelennel."
Nem azzal kell osszevetni, mert a legtobben nem fognak 20-nal tobb probat tenni, mert megunjak. Viszont a kezdeti 4-5 probalkozas a specialis (sot, szerintem extrem) modon valasztott feladat miatt varhatoan pozitiv valaszt fog adni, ami eleg ahhoz, hogy eltorzitsa az eredmenyt.
"Egyre inkább az az érzésem, hogy az motivál benneteket, hogy nektek is kevés negatív próbátok volt, és meg vagytok sértődve, hogy valaki azt mondja, hogy nálatok is lehetett bias. Még mit nem! A feladat volt rossz! Na persze."
Ez az erv szanalmas. Egyreszt ad hominem, masreszt sajat confirmation biasod kivetitese, harmadreszt szerinted ki a fene emlekszik mar, hany negativ probaja volt?? Talan a kitoltok 1%-a.
Nekem halvany fogalmam sincs a sajatomrol. Sot, az 5. probanal mar reg elfelejtettem az 1. probam szamharmasat is, csak annyira emlekeztem, hogy "ezesez a szabaly mar megcafolodott". Egyebek mellett ezert is hulyeseg a pozitiv probak szamabol confirmation biasra kovetkeztetni.
Nem azzal kell osszevetni, mert a legtobben nem fognak 20-nal tobb probat tenni, mert megunjak. Viszont a kezdeti 4-5 probalkozas a specialis (sot, szerintem extrem) modon valasztott feladat miatt varhatoan pozitiv valaszt fog adni, ami eleg ahhoz, hogy eltorzitsa az eredmenyt.
"Egyre inkább az az érzésem, hogy az motivál benneteket, hogy nektek is kevés negatív próbátok volt, és meg vagytok sértődve, hogy valaki azt mondja, hogy nálatok is lehetett bias. Még mit nem! A feladat volt rossz! Na persze."
Ez az erv szanalmas. Egyreszt ad hominem, masreszt sajat confirmation biasod kivetitese, harmadreszt szerinted ki a fene emlekszik mar, hany negativ probaja volt?? Talan a kitoltok 1%-a.
Nekem halvany fogalmam sincs a sajatomrol. Sot, az 5. probanal mar reg elfelejtettem az 1. probam szamharmasat is, csak annyira emlekeztem, hogy "ezesez a szabaly mar megcafolodott". Egyebek mellett ezert is hulyeseg a pozitiv probak szamabol confirmation biasra kovetkeztetni.
Szilágyi András 2008.05.11. 01:26:51
tamás, én veled nem akarok vitatkozni, mert olyan, mintha a falnak beszélnék. Ugyanott tartasz, mint százötven hozzászólással ezelőtt, bebetonoztad magad a véleményedbe. Nem, nem fogom a te kedvedért elismételni az összes korábbi érvelést újra, mert fárasztó és úgysem használ.
nyari mikulas (törölt) 2008.05.11. 01:30:24
Bela2: Nekem a presztizsem nem mulik azon, hogy Andras helyesen ertelmezi-e a kiserleti adatait, vagy sem.
Itt a szkeptikusoknak ugy illene, hogy ne a presztizs, ne a tekintelytisztelet, hanem az igazsag keresese motivaljon.
Lehet, hogy tevedek. De egyelore meg vagyok gyozodve a sajat allaspontomrol. Azert utkoztetem az erveket, hogy magam szamara kideruljon, felreertek-e valamit, ha igen mit, miert.
Ebbol tanulnek.
Kuatato vagyok, szakmam kiserletek tervezese. Ennek nagyon fontos resze a negativ kontroll kiserletek alkalmazasa. Nem tudom elegge hangsulyozni a negativ kontrollok fontossagat. De nem latom be, hogy miert hatranyos az, tobb poztiv kimenetelu kiserletet vegzek, mint olyat, aminek negativ az eredmenye.
Ha az igazsag az, hogy 50%-ban kell sikertelen, negativ eredmenyu kiserletet vegezni (ez a fenti kiserlet allitasa Andras szerint, ha jol ertem), vagy akar csak 50%-ban kell negativ kontrollt tervezni (ez az en olvasatom a megerositesi tevedesrol), akkor szeretnem megerteni, hogy miert, es utana magam is alkalmaznam, es tanitanam azoknak, akikkel egyutt dolgozok.
Ennyi.
Ha valaki latja miben tevedek, es veszi a faradsagot, hogy ramutasson, megkoszonom.
Itt a szkeptikusoknak ugy illene, hogy ne a presztizs, ne a tekintelytisztelet, hanem az igazsag keresese motivaljon.
Lehet, hogy tevedek. De egyelore meg vagyok gyozodve a sajat allaspontomrol. Azert utkoztetem az erveket, hogy magam szamara kideruljon, felreertek-e valamit, ha igen mit, miert.
Ebbol tanulnek.
Kuatato vagyok, szakmam kiserletek tervezese. Ennek nagyon fontos resze a negativ kontroll kiserletek alkalmazasa. Nem tudom elegge hangsulyozni a negativ kontrollok fontossagat. De nem latom be, hogy miert hatranyos az, tobb poztiv kimenetelu kiserletet vegzek, mint olyat, aminek negativ az eredmenye.
Ha az igazsag az, hogy 50%-ban kell sikertelen, negativ eredmenyu kiserletet vegezni (ez a fenti kiserlet allitasa Andras szerint, ha jol ertem), vagy akar csak 50%-ban kell negativ kontrollt tervezni (ez az en olvasatom a megerositesi tevedesrol), akkor szeretnem megerteni, hogy miert, es utana magam is alkalmaznam, es tanitanam azoknak, akikkel egyutt dolgozok.
Ennyi.
Ha valaki latja miben tevedek, es veszi a faradsagot, hogy ramutasson, megkoszonom.
nyari mikulas (törölt) 2008.05.11. 01:32:50
Andras: en is igy latom, hogy olyan, mintha a falnak beszélnék. Ugyanott tartasz, mint százötven hozzászólással ezelőtt, bebetonoztad magad a véleményedbe.
En megprobalom mas oldalrol megvilagitani, miert gondolom ugy.
Nagyon sajnalom, hogy farasztalak.
En megprobalom mas oldalrol megvilagitani, miert gondolom ugy.
Nagyon sajnalom, hogy farasztalak.
bela2 2008.05.11. 01:38:04
Tamas, leegyszerusitve: Ha valamit bizonyitani akarsz, akkor eleg a (sok v. nehany) pozitiv eredmenyu kiserlet. Ha cafolni, akkor a negativ kimenetelueken van a hangsuly. Ha ismeretlent meghatarozni, akkor lenyeges mindketto. Hogy tudd, hol a hatar a jo es rossz kozott. A fenti teszt arrol szolt, hogy ha sokszor (tobbszor) kapok pozitiv visszaigazolast a feltetelezett velemenyemre, hajlamos vagyok igaznak erezni. Pedig kereshetnek (es ha alaposan keresek, talalhatnek) cafolatokat is. De azokat nem szeretjuk annyira.
nyari mikulas (törölt) 2008.05.11. 01:43:15
Bela2 utolso hozzaszolasoddal egyetertek. Nem ezt vitatjuk.
A vita targya, egyfelol, az,
-hogy a pozitiv/negativ valaszok aranya meroszama-e a megerositesi tevedesnek, *
masfelol az,
-hogy ebben a konkret esetben, vagy altalaban pontosan 50% negativ valasz-e az optimalis a feladat helyes megoldasahoz
* a feladat valoban szemleltette amit irsz, de paran ugy veljuk, hogy a kapott negativ/poztiv valaszok aranya ennek nem meroszama.
A vita targya, egyfelol, az,
-hogy a pozitiv/negativ valaszok aranya meroszama-e a megerositesi tevedesnek, *
masfelol az,
-hogy ebben a konkret esetben, vagy altalaban pontosan 50% negativ valasz-e az optimalis a feladat helyes megoldasahoz
* a feladat valoban szemleltette amit irsz, de paran ugy veljuk, hogy a kapott negativ/poztiv valaszok aranya ennek nem meroszama.
nyari mikulas (törölt) 2008.05.11. 01:47:16
Ujraolvasva: "Ha valamit bizonyitani akarsz, akkor eleg a (sok v. nehany) pozitiv eredmenyu kiserlet."
Amikor valami ismeretlent akarok meghatarozni, peldaul ebben a feladatban a szabalyt, akkor ranezek, van egy otletem, hogy mi lehet szabaly es azt probalom bizonyitani. Ehhez, mint ez a feladat nagyon jol megvilagitja, nem elegsegesek a pozitiv eredmenyu kiserletek.
Ezt a feladatot nem lehet helyesen megoldani negativ eredmenyu probalkozasok nelkul.
Ilyen szempontbol nagyon tanulsagos.
Amikor valami ismeretlent akarok meghatarozni, peldaul ebben a feladatban a szabalyt, akkor ranezek, van egy otletem, hogy mi lehet szabaly es azt probalom bizonyitani. Ehhez, mint ez a feladat nagyon jol megvilagitja, nem elegsegesek a pozitiv eredmenyu kiserletek.
Ezt a feladatot nem lehet helyesen megoldani negativ eredmenyu probalkozasok nelkul.
Ilyen szempontbol nagyon tanulsagos.
bela2 2008.05.11. 01:48:21
Mivel a tulnyomo tobbseg megelegedett a kezdeti kusza probalkozasok kiertekelesevel es nem torodott a hatarkeresessel, a meroszam jogos. Mar csak azert is, mert ti is megegyeztetek, hogy lenyegesen tobb hibas szamharmas letezik, mint megfelelo, megis a pozitiv probak voltak tobben. A tobbseg elofeltetelezesekkel elt, amiket bizonyitott (pozitiv iranyban). Ez mi mas, ha nem bias?
nyari mikulas (törölt) 2008.05.11. 02:48:24
Bela2:
Megprobalom mashogy kifejteni, hogy szerintem miert kell tobb pozitiv valszt ado proba, mint negativ.
Eloszor is, amig nem talalom meg a valodi szabalyt, addig meg azok a kerdesek, amikkel cafolni szeretnem a pillanatnyi hipotezisemet, azok egy resze is poztiv valaszt ad.
Kiindulok abbol, hogy nyilvan a 2,4,6,8,10... szamsor a megoldas.
Tesztelem: 4,6,8 10,12,14 stb
Megprobalok egy hibas peldat:
2,4,10 ezt a szamitogep helyesnek iteli, ott szamolja, pedig ez egy "falszifikacio" ez olyan proba volt aminek a szandeka a hipotezisem cafoltat volt, es sikeresen cafoltam a hipotezist.
Nem veletlen, hogy "Wason minden számhármashoz indoklást kért".
En a bias definiciojabol kiindulva azt a szamharmast tekintettem volna pozitivnak, amelyik megfelel az eppen vizsgalt hipotezisnek.
(Andras: mi a velemenyed errol: Talan hogy azert nem ertjuk egymast, mert en azt mondom, hogy ez meroszam a bias, Te meg azt mondod, hogy ez a meroszam jol korrelal a "nem helyes" valaszok szamaval?
Ha igy gondolod, akkor egyetertunk.)
Korabban Andras tett egy nagyon erdekes megjegyzest.
"De mi van, ha én most elárulom, hogy hazudtam, nem az volt a szabály, hogy növekvő számsort kell megadni, hanem azt, hogy vagy növekvő számsort kell megadni, vagy mínusz ezernél kisebb tetszőleges számokat?"
Gondold ezt tovabb. Mi lett volna, ha a szabaly az, barmilyen tetszoleges szamharmas megfelel? Minden proba "megfelel" valaszt eredmenyezett volna.
Mi lett volna, ha az a szabaly az, hogy csak a 2,4,6 szamok ebben sorrenben? Nagyon magas lett volna a "nem felel meg valaszok" aranya.
Tehat nem a "megfelel" es "nem felel meg" valaszok aranya az ami a biast mutatja.
De ebben a konkret kiserletben a valszok aranya korrelal a biasszal.
Megprobalom mashogy kifejteni, hogy szerintem miert kell tobb pozitiv valszt ado proba, mint negativ.
Eloszor is, amig nem talalom meg a valodi szabalyt, addig meg azok a kerdesek, amikkel cafolni szeretnem a pillanatnyi hipotezisemet, azok egy resze is poztiv valaszt ad.
Kiindulok abbol, hogy nyilvan a 2,4,6,8,10... szamsor a megoldas.
Tesztelem: 4,6,8 10,12,14 stb
Megprobalok egy hibas peldat:
2,4,10 ezt a szamitogep helyesnek iteli, ott szamolja, pedig ez egy "falszifikacio" ez olyan proba volt aminek a szandeka a hipotezisem cafoltat volt, es sikeresen cafoltam a hipotezist.
Nem veletlen, hogy "Wason minden számhármashoz indoklást kért".
En a bias definiciojabol kiindulva azt a szamharmast tekintettem volna pozitivnak, amelyik megfelel az eppen vizsgalt hipotezisnek.
(Andras: mi a velemenyed errol: Talan hogy azert nem ertjuk egymast, mert en azt mondom, hogy ez meroszam a bias, Te meg azt mondod, hogy ez a meroszam jol korrelal a "nem helyes" valaszok szamaval?
Ha igy gondolod, akkor egyetertunk.)
Korabban Andras tett egy nagyon erdekes megjegyzest.
"De mi van, ha én most elárulom, hogy hazudtam, nem az volt a szabály, hogy növekvő számsort kell megadni, hanem azt, hogy vagy növekvő számsort kell megadni, vagy mínusz ezernél kisebb tetszőleges számokat?"
Gondold ezt tovabb. Mi lett volna, ha a szabaly az, barmilyen tetszoleges szamharmas megfelel? Minden proba "megfelel" valaszt eredmenyezett volna.
Mi lett volna, ha az a szabaly az, hogy csak a 2,4,6 szamok ebben sorrenben? Nagyon magas lett volna a "nem felel meg valaszok" aranya.
Tehat nem a "megfelel" es "nem felel meg" valaszok aranya az ami a biast mutatja.
De ebben a konkret kiserletben a valszok aranya korrelal a biasszal.
nyari mikulas (törölt) 2008.05.11. 05:51:03
folytatas:
Masodszor, egy szabaly tesztelesenel tobb pozitiv probat is teszek, amelyek a szabaly ervenyessegi koret tisztazzak.
Az elozo peldanal maradva, a 2,4,6,8,10... feltevest ellenoriznem kell nagy szamokra, nagyon nagy samokra nullat tartalmazo szamharmasokra es negativ szamokra is.
Ugyanakkor egyetlen nemleges valasz elegendo ahhoz, hogy egy hipotezist elvessek, ha peldaul latom, hogy a 4,6,10 helyes, akkor egyetlen lepesben elvetem a hipotezist, es ujat kezdek tesztelni.
Tehat tobb oka is van annak, hogy tobb pozitiv kimenetelu valaszt tesztelek, ezek egy resze nem a bias kovetkezmenye, a kiserlet megis oda szamolja.
Masodszor, egy szabaly tesztelesenel tobb pozitiv probat is teszek, amelyek a szabaly ervenyessegi koret tisztazzak.
Az elozo peldanal maradva, a 2,4,6,8,10... feltevest ellenoriznem kell nagy szamokra, nagyon nagy samokra nullat tartalmazo szamharmasokra es negativ szamokra is.
Ugyanakkor egyetlen nemleges valasz elegendo ahhoz, hogy egy hipotezist elvessek, ha peldaul latom, hogy a 4,6,10 helyes, akkor egyetlen lepesben elvetem a hipotezist, es ujat kezdek tesztelni.
Tehat tobb oka is van annak, hogy tobb pozitiv kimenetelu valaszt tesztelek, ezek egy resze nem a bias kovetkezmenye, a kiserlet megis oda szamolja.
bela2 2008.05.11. 09:30:51
Tamas, kerlek szakadj el a konkret peldatol es ertsd meg az elmeletet. Ha azt erted, erteni fogod a pelda altal mutatott vetuletet is.
Az elmeletben vegtelen szamu fekete es feher pont van. Ez igy van a peldaban is, vegtelen szamu jo es rossz szamharmas letezik. Ha barmelyik mezot egy (vagy veges) pontra korlatozod, akkor jo nagyot torzitasz az elmeleten. Ott mar csak torzitva lehetne merni a torzitast :-), de a trend valoszinuleg ott is latszana.
Az elmeletben vegtelen szamu fekete es feher pont van. Ez igy van a peldaban is, vegtelen szamu jo es rossz szamharmas letezik. Ha barmelyik mezot egy (vagy veges) pontra korlatozod, akkor jo nagyot torzitasz az elmeleten. Ott mar csak torzitva lehetne merni a torzitast :-), de a trend valoszinuleg ott is latszana.
bela2 2008.05.11. 09:40:16
Masreszt hiaba ellenorzod a sajat szabalyod negativ iranyban, ha a kiserlet pozitiv eredmenyt hoz. Attol meg a fekete tartomany belsejeben jarsz, nem a hatarokat feszegeted. Meg az egyszeru szabalynal is "foldhozragadtabb" feltevesekkel elsz, amit cafolni probalsz, de nem sikerul. Kicsit tullepve a terkepes peldan: ket dimenzioban keresed a megoldast, es elfogadod a sik egyik felet (vagy hatodat), de eszedbe sem jut harom dimenzioban gondolkodni. (Ne haborodj fel, nem matematikai a lekepezesem, ugy persze nem igaz, de probalok koltoi kepeket hasznalni...)
nyari mikulas (törölt) 2008.05.11. 13:29:45
Bela, az elmeletet ugy gondolom ertem, es elfogadom, nem vitatom.
Amit vitatunk, hogy a kapott poztiv (megerosito, feher) valaszok, vagy pedig az elvart poztiv (megerosito, feher) valaszok aranya mutatja-e a megerositesi torzitast?
Amit en szinten vitatok, hogy altalaban, 50% kapott vagy elvart (itt mindegy, mivel szerintem egyik sem) poztiv (megerosito, feher) valasz arany-e a torzitasnentesseg feltetele?
Ugy gondolom, hogy te arrol irsz, hogy helyes valasz megtalalasahoz szukseges elegendoen magas szamu helyes es heyltelen (vagy fekete es feher) valasz ismerete.
Egyetertunk.
Tegyuk fel, hogy a hatarvonalnak az a szakasza amit terkepeznunk kell a fekete es a feher terulet kozott egy egyenes.
Valoban az a leghatekonyabb, leggyorsabb strategia, hogy cikk-cakkban haladsz, ahanyszor fekete teruletre ersz a feherbol, fordulsz, es viszont.
Mivel egy rovid es egyenes szakaszt terkepezel, 7 pont az egyik oldalon es 7 a masikon eleg jol meghatarozza a vonalat.
Amit en nem latok be, hogy mi a kulonbseg a kovetkezo harom megoldas kozott:
A 14 pontot nezett meg, 7 feheret es het feketet.
B 114 pontot nezett meg 107 feheret es 7 feketet (megnezte ugyanazt a het-het pontot amiket A es ezen kivul meg megnezett 100 masikat, amik mind feherek voltak).
C 114 pontot nezett meg 7 feheret es 107 feketet (megnezte ugyanazt a het-het pontot amiket A es ezen kivul meg megnezett 100 masikat, amik mind feketek voltak).
Szerintem A, B es C ugyanazt a hatart fogja lerajzolni mint A. Nem fog torzulni a hatarrol az elkepzelesuk attol, hogy ismernek tovabbi 100 pontot, amikrol tudjak, hogy nem hatar.
Amit vitatunk, hogy a kapott poztiv (megerosito, feher) valaszok, vagy pedig az elvart poztiv (megerosito, feher) valaszok aranya mutatja-e a megerositesi torzitast?
Amit en szinten vitatok, hogy altalaban, 50% kapott vagy elvart (itt mindegy, mivel szerintem egyik sem) poztiv (megerosito, feher) valasz arany-e a torzitasnentesseg feltetele?
Ugy gondolom, hogy te arrol irsz, hogy helyes valasz megtalalasahoz szukseges elegendoen magas szamu helyes es heyltelen (vagy fekete es feher) valasz ismerete.
Egyetertunk.
Tegyuk fel, hogy a hatarvonalnak az a szakasza amit terkepeznunk kell a fekete es a feher terulet kozott egy egyenes.
Valoban az a leghatekonyabb, leggyorsabb strategia, hogy cikk-cakkban haladsz, ahanyszor fekete teruletre ersz a feherbol, fordulsz, es viszont.
Mivel egy rovid es egyenes szakaszt terkepezel, 7 pont az egyik oldalon es 7 a masikon eleg jol meghatarozza a vonalat.
Amit en nem latok be, hogy mi a kulonbseg a kovetkezo harom megoldas kozott:
A 14 pontot nezett meg, 7 feheret es het feketet.
B 114 pontot nezett meg 107 feheret es 7 feketet (megnezte ugyanazt a het-het pontot amiket A es ezen kivul meg megnezett 100 masikat, amik mind feherek voltak).
C 114 pontot nezett meg 7 feheret es 107 feketet (megnezte ugyanazt a het-het pontot amiket A es ezen kivul meg megnezett 100 masikat, amik mind feketek voltak).
Szerintem A, B es C ugyanazt a hatart fogja lerajzolni mint A. Nem fog torzulni a hatarrol az elkepzelesuk attol, hogy ismernek tovabbi 100 pontot, amikrol tudjak, hogy nem hatar.
bela2 2008.05.11. 13:42:11
OK, kozelitsuk meg masfelol.
Minel tobb pontot talalsz egy alakzatrol, annal tobbet tudsz mondani a belsejerol, merthogy a pontok mindig belulrol szarmaznak. Ha eleg sok egyszinu pontod van, bekarikazod oket, es rajuk huzol egy szabalyt. De nem tudod, hogy a szabalyod es az ellenkezo szinu pontok KOZOTT mi van.
Egyebkent megint elofeltevessel eltel, es bebizonyitottad, hogy egyenes a hatar. Pedig nem biztos, hogy az.
A fekete vagy eppen feher pontok tulsulya nem jobb vagy rosszabb egymasnal, de mindenkeppen rosszabb az egyensulynal. Vagyis torzulas. A kiserlet azt mutatta, hogy-hogynem jellemzo a pozitiv torzulas, mert ilyen az emberi termeszet.
Minel tobb pontot talalsz egy alakzatrol, annal tobbet tudsz mondani a belsejerol, merthogy a pontok mindig belulrol szarmaznak. Ha eleg sok egyszinu pontod van, bekarikazod oket, es rajuk huzol egy szabalyt. De nem tudod, hogy a szabalyod es az ellenkezo szinu pontok KOZOTT mi van.
Egyebkent megint elofeltevessel eltel, es bebizonyitottad, hogy egyenes a hatar. Pedig nem biztos, hogy az.
A fekete vagy eppen feher pontok tulsulya nem jobb vagy rosszabb egymasnal, de mindenkeppen rosszabb az egyensulynal. Vagyis torzulas. A kiserlet azt mutatta, hogy-hogynem jellemzo a pozitiv torzulas, mert ilyen az emberi termeszet.
frank 2008.05.11. 13:46:33
szerintem ez a fekete alakzat analogia nem tul jo. a konkret feladatban szamharmasok egy reszhalmazat kellett megkeresni, ezek milyen ertelemben alkotnanak osszefuggo alakzatot?? es mi felelne meg a hatarnak?
nyari mikulas (törölt) 2008.05.11. 13:49:18
Hasonlitsd ossze Andras ket abrajat (a cikkben es egy hozzaszolasaban).
A cikkbeli abra azt mutatja, hogy a pontosan het kiserletet vegzo jatekozok eseten a helyes szabaly megtalalasa aranyos volt kapott a nem felel meg (cafolat) valaszok szamaval. A grafikon egyenletesen no 71% cafolatig, amikor is 100%-ban helyes szabalyt allapitanak meg a jatekosok.
Ha ezt a grafikont nezed, akkor arra kell kovetkeztess, hogy ketszer tobb cafolat kell a helyes valaszhoz.
Ha nadras kesobb elkeszitett abrajat nezed, azon az osszes jatekost feldolgozta, ott szkeptikus.blog.hu/media/image/negarany.gif 30 es 55% megerosito valasz alapjan kozel ugyannyi volt a helyes megfejtes, a legmagasabb epp 50% megerosito valasz eseten.
Egy harmadik szam: az osszes helyesen valaszolot egyben vizsgalva 35.6% cafolt kerdest kaptunk.
Akkor most 71% vagy 50% vagy 35.6% cafolt valasz szukseges?
Nem az _arany_ az ami szamit szerintem, hanem az, hogy szukseges bizonyos _szamu_ cafolatot kapjunk a helyes megoldashoz. A kiserletben ez legalabb 5 cafolatot jelentett.
A ket abra kozotti kulonbseg abbol adodik, hogy az eso abranal csak azok szerepelnek akik 7 kerdest tettek fel, a masik abran pedig az osszes jatekos, azok is, akik sokkal tobb kerdest tettek fol.
A szamok alatamasztjak azt az elkepzelesemet, hogy nem a cafolt valaszok aranya az ami lenyeges.
A cikkbeli abra azt mutatja, hogy a pontosan het kiserletet vegzo jatekozok eseten a helyes szabaly megtalalasa aranyos volt kapott a nem felel meg (cafolat) valaszok szamaval. A grafikon egyenletesen no 71% cafolatig, amikor is 100%-ban helyes szabalyt allapitanak meg a jatekosok.
Ha ezt a grafikont nezed, akkor arra kell kovetkeztess, hogy ketszer tobb cafolat kell a helyes valaszhoz.
Ha nadras kesobb elkeszitett abrajat nezed, azon az osszes jatekost feldolgozta, ott szkeptikus.blog.hu/media/image/negarany.gif 30 es 55% megerosito valasz alapjan kozel ugyannyi volt a helyes megfejtes, a legmagasabb epp 50% megerosito valasz eseten.
Egy harmadik szam: az osszes helyesen valaszolot egyben vizsgalva 35.6% cafolt kerdest kaptunk.
Akkor most 71% vagy 50% vagy 35.6% cafolt valasz szukseges?
Nem az _arany_ az ami szamit szerintem, hanem az, hogy szukseges bizonyos _szamu_ cafolatot kapjunk a helyes megoldashoz. A kiserletben ez legalabb 5 cafolatot jelentett.
A ket abra kozotti kulonbseg abbol adodik, hogy az eso abranal csak azok szerepelnek akik 7 kerdest tettek fel, a masik abran pedig az osszes jatekos, azok is, akik sokkal tobb kerdest tettek fol.
A szamok alatamasztjak azt az elkepzelesemet, hogy nem a cafolt valaszok aranya az ami lenyeges.
nyari mikulas (törölt) 2008.05.11. 13:56:23
Bela, fennakadsz a reszleteken. Mindegy, hogy milyen alaku a haratvonal, A, B es C ugyanazt a hatart fogja lerajzolni.
Amugy valoban nem jo az analogia a szamokkal vegzett kiserlethez szerintem sem. A megismeresi folyamat mas, a szamoknal szabalyt keresunk, a hatar eseten egy konkret vonalat.
A szamoknal elegendo egy olyan valasz, hogy peldaul barmilyen paratlan szam megfelel, a hatar eseten nincs olyan valasz, hogy barmilyen hullamvonal jo. Vagy a konkret szampelda analogiaja a hatar eseten, hogy minel keletebbre terkepezel keresed, annal inkabb eszak fele gorbul a hatar es mindegy, hogy mennyivel eszakabbra, a lenyeg, hogy a keletebbre levo pontok eszakabbra vannak a nyugati pontoknal. ;-)
Amugy valoban nem jo az analogia a szamokkal vegzett kiserlethez szerintem sem. A megismeresi folyamat mas, a szamoknal szabalyt keresunk, a hatar eseten egy konkret vonalat.
A szamoknal elegendo egy olyan valasz, hogy peldaul barmilyen paratlan szam megfelel, a hatar eseten nincs olyan valasz, hogy barmilyen hullamvonal jo. Vagy a konkret szampelda analogiaja a hatar eseten, hogy minel keletebbre terkepezel keresed, annal inkabb eszak fele gorbul a hatar es mindegy, hogy mennyivel eszakabbra, a lenyeg, hogy a keletebbre levo pontok eszakabbra vannak a nyugati pontoknal. ;-)
Szilágyi András 2008.05.11. 14:12:27
tamás,
az adataim szerint a negatív válaszok aránya jobban korrelál a válasz helyességével, mint az abszolút számuk (0,69 vs. 0,51).
Fölösleges azon lovagolni, hogy 50% vagy 40 vagy 70 az optimum, ez nem ennyire egzakt dolog, más tényezőktől is függ. Van egy korreláció, ennyi. Magasabb próbaszám mellett kisebb arány is elég.
az adataim szerint a negatív válaszok aránya jobban korrelál a válasz helyességével, mint az abszolút számuk (0,69 vs. 0,51).
Fölösleges azon lovagolni, hogy 50% vagy 40 vagy 70 az optimum, ez nem ennyire egzakt dolog, más tényezőktől is függ. Van egy korreláció, ennyi. Magasabb próbaszám mellett kisebb arány is elég.
bela2 2008.05.11. 14:17:39
Lassan le is zarom a borso falra hanyasat.
Probaljatok egy kicsit elvonatkoztatni. Ugymond absztrahalni.
A modellben egy pont = egy szamharmas. A fekete jo, a feher nem (vagy forditva, tokmindegy). A hatarvonal maga a szabaly, amit keresunk. Nem tudjuk, hogy egyenes vagy hullamos, lehet barmilyen.
Minimalis (veges szamu, raadasul keves) kiserlettel nem lehet MEGTALALNI a szabalyt, csak RAHIBAZNI vagy ELRONTANI.
A teszt azt mutatta, hogy szinte mindenkinek lenyegesen tobb pozitiv kiserlete volt, mint negativ, raadasul az elrontoknak aranyaiban meg tobb, mint a rahibazoknak.
Erdekes (termeszetes?) modon megerositesi torzulast MUTATOTT (szamszakilag is) nem pedig cafolatit vagy egyensulyt.
Senki nem allitotta, hogy ez igy rossz. Ez igy van.
Probaljatok egy kicsit elvonatkoztatni. Ugymond absztrahalni.
A modellben egy pont = egy szamharmas. A fekete jo, a feher nem (vagy forditva, tokmindegy). A hatarvonal maga a szabaly, amit keresunk. Nem tudjuk, hogy egyenes vagy hullamos, lehet barmilyen.
Minimalis (veges szamu, raadasul keves) kiserlettel nem lehet MEGTALALNI a szabalyt, csak RAHIBAZNI vagy ELRONTANI.
A teszt azt mutatta, hogy szinte mindenkinek lenyegesen tobb pozitiv kiserlete volt, mint negativ, raadasul az elrontoknak aranyaiban meg tobb, mint a rahibazoknak.
Erdekes (termeszetes?) modon megerositesi torzulast MUTATOTT (szamszakilag is) nem pedig cafolatit vagy egyensulyt.
Senki nem allitotta, hogy ez igy rossz. Ez igy van.
nyari mikulas (törölt) 2008.05.11. 14:17:56
Kosz Andras, igy egyetertunk.
vje 2008.05.11. 14:31:56
"Ti ugy erzitek, konnyu volt megtalalni a szabalyt. A tulnyomo tobbseg viszont nem megtalalta, hanem rahibazott."
A többség...
Komolyan, ebben a kissé felfordult világban ezt a csontot rágjátok?
Ahhelyett, hogy technikákat találnátok arra, hogy egy ilyen lássuk be nem különösebben nagy mentális "erőt" feltételező feladat megoldásában segítsük már azt a sokszázalékot???
Mert ez azért elég nehéz... Ránézni...
Mint az idei érettségi feladatra... Ha egy kiló banán 75 Ft, mennyit vehetsz 300 forintért...
Lehet, hogy nem pontosak azt adatok...
De a lényeg, az adott...
Siralom...
Elemezzülk már ki, hogy miért kellett ezt a feladatot 2008-ban érettségi feladatként az ifjak elé tárni???
Ki, miért, és hogyan reagált, válaszolt erre...
TUDOMÁNYOS barátaim...
A többség...
Komolyan, ebben a kissé felfordult világban ezt a csontot rágjátok?
Ahhelyett, hogy technikákat találnátok arra, hogy egy ilyen lássuk be nem különösebben nagy mentális "erőt" feltételező feladat megoldásában segítsük már azt a sokszázalékot???
Mert ez azért elég nehéz... Ránézni...
Mint az idei érettségi feladatra... Ha egy kiló banán 75 Ft, mennyit vehetsz 300 forintért...
Lehet, hogy nem pontosak azt adatok...
De a lényeg, az adott...
Siralom...
Elemezzülk már ki, hogy miért kellett ezt a feladatot 2008-ban érettségi feladatként az ifjak elé tárni???
Ki, miért, és hogyan reagált, válaszolt erre...
TUDOMÁNYOS barátaim...
Szilágyi András 2008.05.11. 14:37:24
Olvastam még egy csomó szakirodalmat. A Wikipédia igencsak félrevezető, mert rosszul értelmezi a Wason-kísérletet. Az persze igaz, hogy a Wason-kísérletet a confirmation bias klasszikus alapkísérletének tartják. Viszont időközben sikerült rájönniük a kutatóknak, hogy a confirmation szót kétféleképpen lehet érteni: 1. hipotézis megerősítése (szemben a falszifikálással), 2. hipotézis pozitív példával való tesztelése (szemben a negatív példával való teszteléssel). A Wikipédia az 1. értelemben idézi a Wason-kísérletet, viszont a szakirodalom alapján úgy látom, hogy mára már senki nem így értelmezi. A Wason-kísérlet a 2. típusú értelemben igazolt egy biast. Ezt positive-testing biasnak nevezzük, vagyis a hipotéziseinket olyan módon szeretjük tesztelni, hogy pozitív példákat vizsgálunk.
A negatív válaszarány azért korrelál ezzel, mert a Wason-kísérlet esetében a tényleges szabály bővebb, mint a tipikusan használt hipotézisek, és ezért csak negatív teszteléssel lehet nemleges választ kapni.
A confirmation bias egy nem egzaktul definiált fogalom, hanem egy gyűjtőfogalom, amibe sok mindent bedobálnak. Általában a positive-testing biast is az egyik változatának tekintik.
Sok kutató amellett érvel viszont, hogy a positive-testing bias a valóságos szituációk nagy többségében nagyonis helyes stratégia, mert ez biztosítja a legnagyobb esélyt a falszifikációra, és ezért nem véletlen, hogy evolúciósan ez alakult ki, ezt használjuk default stratégiaként. Vannak viszont olyan szituációk, amikor tévútra visz, ilyen a Wason-kísérlet szituációja is.
A negatív válaszarány azért korrelál ezzel, mert a Wason-kísérlet esetében a tényleges szabály bővebb, mint a tipikusan használt hipotézisek, és ezért csak negatív teszteléssel lehet nemleges választ kapni.
A confirmation bias egy nem egzaktul definiált fogalom, hanem egy gyűjtőfogalom, amibe sok mindent bedobálnak. Általában a positive-testing biast is az egyik változatának tekintik.
Sok kutató amellett érvel viszont, hogy a positive-testing bias a valóságos szituációk nagy többségében nagyonis helyes stratégia, mert ez biztosítja a legnagyobb esélyt a falszifikációra, és ezért nem véletlen, hogy evolúciósan ez alakult ki, ezt használjuk default stratégiaként. Vannak viszont olyan szituációk, amikor tévútra visz, ilyen a Wason-kísérlet szituációja is.
bela2 2008.05.11. 15:02:51
Kedves vje!
Az erettsegi feladatttal kapcsolatos haborgasoddal egyetertek, en is hallottam ilyesmit, ha igaz, tenyleg botranyos.
Amit felreertesz: ez a blogbejegyzes nem matematikai feladvany volt, hanem pszichologiai kiserlet. Nem a megtalalt szabaly a vita targya, hanem a kiserleti eredmenyek kiertekelese.
Az erettsegi feladatttal kapcsolatos haborgasoddal egyetertek, en is hallottam ilyesmit, ha igaz, tenyleg botranyos.
Amit felreertesz: ez a blogbejegyzes nem matematikai feladvany volt, hanem pszichologiai kiserlet. Nem a megtalalt szabaly a vita targya, hanem a kiserleti eredmenyek kiertekelese.
hvuk 2008.05.11. 23:05:10
Hú, vazzeg, termeltek rendesen! Mostantól pontokba szedve fogok vitázni, mert csak úgy van értelme szerintem, úgy nem fogunk egymás mellett elbeszélni. Kérek mindekit, hogy jelölje meg a válaszában, hogy melyik pontomra reflektál!
1. Nem értem miért volt szükséges mind az eredeti, mind András kísérletében induló számhármast definiálni. Ez erősen torzította szerintem a kísérlet kimentelét és bármiféle közölt számhármas nélkül tisztább képet kaptunk volna.
2. András azt állítja, hogy a szabálytól nem függ az optimális pozitív-negatív arány, az mindig 50% (feltéve, hogy mind a megfelelő, mind a nem megfelelő számhármasok száma végtelen). Kaphatnánk erre bármiféle bizonyítást?
3. András kedvence a fehér alapon fekete négyzet példája. Módosítsuk ezt a feladatot egy kicsit úgy, hogy jobban igazodjon az aktuálishoz.- Legyen adva egy 1 oldalhosszú négyzet, amiben elrejtettünk 1 vagy több fekete négyzetet. Koordináták megadásával tesztelhetjük, hogy az adott pont fekete vagy fehér. A végén az a feladat, hogy megadjuk, hogy pontosan hol vannak fekete neégyzetek. A koordináták tetszőleges 0 és 1 közötti valós számok lehetnek.
"A" kísérlet: Legyen mindössze egy fekete négyzet, amely fedje a papír 5%-át. Ebben az esetben triviálisan lényegesen több fehér pontot fog a kísérletező lekérdezni, mint feketét.
"B" kísérlet: Fedje a papír területének kb. felét fekete négyzet. Ekkor kb. egálban lesznek a fekete és a fehér részbe eső tesztelt számhármasok száma.
"C" kísérlet: Fedje a papír 95%-át fekete négyzet. Ekkor triviálisan lényegesen több fekete pont tesztelése lesz az optimális.
4. Miért tesszük fel, hogy a kísérletezők emlékeznek a régebbi számhármasokra?
5. Mi van olyan kísérletnél, ahol a kiinduló számhármas a 2, 4, 6 és a szabály az, hogy csak a k, k+2, k+4 alakú számhármasok a jók?
6. Mi lenne vajon a végkifejlete egy olyan kísérletnek, ahol a szabály az, hogy a számhármas vagy a 2, 4, 6 vagy pedig csupa negatív számból áll? Van egy olyan sejtésem, hogy egy szemernyi confirmation bias nem lépne fel, a tesztelt számhármasok döntő többsége nem felelne meg a szabálynak.
1. Nem értem miért volt szükséges mind az eredeti, mind András kísérletében induló számhármast definiálni. Ez erősen torzította szerintem a kísérlet kimentelét és bármiféle közölt számhármas nélkül tisztább képet kaptunk volna.
2. András azt állítja, hogy a szabálytól nem függ az optimális pozitív-negatív arány, az mindig 50% (feltéve, hogy mind a megfelelő, mind a nem megfelelő számhármasok száma végtelen). Kaphatnánk erre bármiféle bizonyítást?
3. András kedvence a fehér alapon fekete négyzet példája. Módosítsuk ezt a feladatot egy kicsit úgy, hogy jobban igazodjon az aktuálishoz.- Legyen adva egy 1 oldalhosszú négyzet, amiben elrejtettünk 1 vagy több fekete négyzetet. Koordináták megadásával tesztelhetjük, hogy az adott pont fekete vagy fehér. A végén az a feladat, hogy megadjuk, hogy pontosan hol vannak fekete neégyzetek. A koordináták tetszőleges 0 és 1 közötti valós számok lehetnek.
"A" kísérlet: Legyen mindössze egy fekete négyzet, amely fedje a papír 5%-át. Ebben az esetben triviálisan lényegesen több fehér pontot fog a kísérletező lekérdezni, mint feketét.
"B" kísérlet: Fedje a papír területének kb. felét fekete négyzet. Ekkor kb. egálban lesznek a fekete és a fehér részbe eső tesztelt számhármasok száma.
"C" kísérlet: Fedje a papír 95%-át fekete négyzet. Ekkor triviálisan lényegesen több fekete pont tesztelése lesz az optimális.
4. Miért tesszük fel, hogy a kísérletezők emlékeznek a régebbi számhármasokra?
5. Mi van olyan kísérletnél, ahol a kiinduló számhármas a 2, 4, 6 és a szabály az, hogy csak a k, k+2, k+4 alakú számhármasok a jók?
6. Mi lenne vajon a végkifejlete egy olyan kísérletnek, ahol a szabály az, hogy a számhármas vagy a 2, 4, 6 vagy pedig csupa negatív számból áll? Van egy olyan sejtésem, hogy egy szemernyi confirmation bias nem lépne fel, a tesztelt számhármasok döntő többsége nem felelne meg a szabálynak.
hvuk 2008.05.11. 23:06:26
Fent a 3. pontban a "papír" szó helyett fehér négyzetet kell érteni. Bocsi, a félreérthető fogalmazásért.
hvuk 2008.05.11. 23:07:54
Bela2!
"Tamas, kerlek szakadj el a konkret peldatol es ertsd meg az elmeletet. Ha azt erted, erteni fogod a pelda altal mutatott vetuletet is.
Az elmeletben vegtelen szamu fekete es feher pont van. Ez igy van a peldaban is, vegtelen szamu jo es rossz szamharmas letezik. Ha barmelyik mezot egy (vagy veges) pontra korlatozod, akkor jo nagyot torzitasz az elmeleten. Ott mar csak torzitva lehetne merni a torzitast :-), de a trend valoszinuleg ott is latszana."
Szerencsére a fenti 3-as példámban nem estem bele a fenti hibába. Minden esetben végtelen mennyiségű fehér és fekete pont van.
"Tamas, kerlek szakadj el a konkret peldatol es ertsd meg az elmeletet. Ha azt erted, erteni fogod a pelda altal mutatott vetuletet is.
Az elmeletben vegtelen szamu fekete es feher pont van. Ez igy van a peldaban is, vegtelen szamu jo es rossz szamharmas letezik. Ha barmelyik mezot egy (vagy veges) pontra korlatozod, akkor jo nagyot torzitasz az elmeleten. Ott mar csak torzitva lehetne merni a torzitast :-), de a trend valoszinuleg ott is latszana."
Szerencsére a fenti 3-as példámban nem estem bele a fenti hibába. Minden esetben végtelen mennyiségű fehér és fekete pont van.
bela2 2008.05.11. 23:21:04
hvuk: nem igazan ertelek. Miert peldalozol kitalalt feladatokkal, ha a valosagban tesztelt es publikalt feladat megcafolja az ervelesed? A novekvo szamharmasok kevesebb, mint 16%-at fedik a negyzetednek. Most nem szeretnek a pontos erteknek utanaszamolni, a kevesebb mint 1/6-dal nagyjabol mindenki egyetertett. Es megis lenyegesen tobb megerosito kiserlet szuletett, mint az 5/6 reszt lefedo cafolati tartomanyra. Ez a bias.
hvuk 2008.05.11. 23:21:39
Bela2!
"A kiserlet azt mutatta, hogy-hogynem jellemzo a pozitiv torzulas, mert ilyen az emberi termeszet."
1. Nem, a kísérlet azt mutatta meg, hogy az adott kiindulási helyzetben (adott számhármas és adott szabály) ez volt a jellemző. Ebből egyáltalán nem következik, hogy ez általános lenne.
2. Sőt, érdekes dolog, hogy nem egy üres "fehér lappal" kezdtek (nincs kiinduló számhármas), hanem eleve torzítást vittek a rendszerbe a kezdeti számhármas megadásával.
3. Érdekes dolog, hogy András azt mondja, hogy az összes kísérletet egyben kell vizsgálni és annak kellene 50-50%-ban pozitív és negatívnak lennie. De mi van, ha a kísérletet végzőknél egy másik pszichológia jelenség is fellépett, mégpedig a "múltbeli kísérletek ignorálása" nevű. Ez az a jelenség, ahol a múltbeli kísérleteket nem veszik figyelembe, ha az nem a jelenleg feltett szabály megcáfolására vagy megerősítésére volt végrehajtva. Azaz ha végeztem mondjuk 10 számtesztet (8 pozitív, 2 negatív), amíg eljutottam a végül elküldött szabályig (mindegy, hogy az jó-e vagy sem), akkor amikor azt kezdtem tesztelni, akkor az előző kísérleteket egyszerűen nem vettem figyelembe, azaz a szabályt elölről kezdtem tesztelni. Triviálisan igaz, hogy egy ilyen - mellesleg szerintem létező - jelenség feltételezése után a várható pozitav-negatív arány már elvileg sem lehet 50%-os.
"A kiserlet azt mutatta, hogy-hogynem jellemzo a pozitiv torzulas, mert ilyen az emberi termeszet."
1. Nem, a kísérlet azt mutatta meg, hogy az adott kiindulási helyzetben (adott számhármas és adott szabály) ez volt a jellemző. Ebből egyáltalán nem következik, hogy ez általános lenne.
2. Sőt, érdekes dolog, hogy nem egy üres "fehér lappal" kezdtek (nincs kiinduló számhármas), hanem eleve torzítást vittek a rendszerbe a kezdeti számhármas megadásával.
3. Érdekes dolog, hogy András azt mondja, hogy az összes kísérletet egyben kell vizsgálni és annak kellene 50-50%-ban pozitív és negatívnak lennie. De mi van, ha a kísérletet végzőknél egy másik pszichológia jelenség is fellépett, mégpedig a "múltbeli kísérletek ignorálása" nevű. Ez az a jelenség, ahol a múltbeli kísérleteket nem veszik figyelembe, ha az nem a jelenleg feltett szabály megcáfolására vagy megerősítésére volt végrehajtva. Azaz ha végeztem mondjuk 10 számtesztet (8 pozitív, 2 negatív), amíg eljutottam a végül elküldött szabályig (mindegy, hogy az jó-e vagy sem), akkor amikor azt kezdtem tesztelni, akkor az előző kísérleteket egyszerűen nem vettem figyelembe, azaz a szabályt elölről kezdtem tesztelni. Triviálisan igaz, hogy egy ilyen - mellesleg szerintem létező - jelenség feltételezése után a várható pozitav-negatív arány már elvileg sem lehet 50%-os.
hvuk 2008.05.11. 23:23:43
Bela2:
Azért példálózok más feladattal, mert nem azt vitatom, hogy van confirmation bias, hanem azt, hogy mindenképpen 50% lenne a helyes pozitv-negatív kimeneteli arány. Ez az amit András nagyvonaúan feltett, mindenféle bizonyítás nélkül.
Azért példálózok más feladattal, mert nem azt vitatom, hogy van confirmation bias, hanem azt, hogy mindenképpen 50% lenne a helyes pozitv-negatív kimeneteli arány. Ez az amit András nagyvonaúan feltett, mindenféle bizonyítás nélkül.
bela2 2008.05.11. 23:27:43
OK. Akkor az 50%-ot ne hidd el, pedig annyi az elmelet. Hidd el a sajat 16-84%-odat. Kimutatta a teszt a biast? Meg erosebben is, mint kellene...
hvuk 2008.05.11. 23:30:15
"Sok kutató amellett érvel viszont, hogy a positive-testing bias a valóságos szituációk nagy többségében nagyonis helyes stratégia, mert ez biztosítja a legnagyobb esélyt a falszifikációra, és ezért nem véletlen, hogy evolúciósan ez alakult ki, ezt használjuk default stratégiaként. Vannak viszont olyan szituációk, amikor tévútra visz, ilyen a Wason-kísérlet szituációja is."
Na végre! Csak azt nem értem, hgoy ezt nekünk miért nem lehetett elhinni. Ezzel a teljes hozzászólásoddal egyetértek. Feltéve, persze, hogy jól értem. :)
Amúgy ez az egész visszamegy a "szabály" szó értelmezésére. Egy algoritmus tesztelésére nyilván a pozitív testing-bias a helyes (mint ezt fentebb le is írtam, de eléggé ignorálva volt). És mindennapi életünkben az algoritmus típusú feladatok fordulnak elő döntő többségében.
Na végre! Csak azt nem értem, hgoy ezt nekünk miért nem lehetett elhinni. Ezzel a teljes hozzászólásoddal egyetértek. Feltéve, persze, hogy jól értem. :)
Amúgy ez az egész visszamegy a "szabály" szó értelmezésére. Egy algoritmus tesztelésére nyilván a pozitív testing-bias a helyes (mint ezt fentebb le is írtam, de eléggé ignorálva volt). És mindennapi életünkben az algoritmus típusú feladatok fordulnak elő döntő többségében.
hvuk 2008.05.11. 23:33:33
Bela2!
Egész pontosan milyen elmélet szerint kell annyi? Ha a feladat úgy szól, hogy találja meg azt a determinisztikus algoritmust, amely előállítja a 2, 4, 6 számhármast és amely tesztelhető a fenti alkalmazással (amit András csinált), akkor garantálom neked, hogy nem az 50-50% lesz még az elvileg helyes megoldás sem.
Egész pontosan milyen elmélet szerint kell annyi? Ha a feladat úgy szól, hogy találja meg azt a determinisztikus algoritmust, amely előállítja a 2, 4, 6 számhármast és amely tesztelhető a fenti alkalmazással (amit András csinált), akkor garantálom neked, hogy nem az 50-50% lesz még az elvileg helyes megoldás sem.
hvuk 2008.05.11. 23:34:43
Tényleg, az "elmélet"-ből hogyan jön ki az 50-50%? És milyen "elmélet"-ből jön ki? Én még ilyen elméletről nem hallottam, de nem ismerem az összeset. Tudnál linket adni rá?
bela2 2008.05.11. 23:38:18
1. strategia: Es ki mondta, hogy rossz a bias-os gondolkodas? Nyilvan elmeletileg nem korrekt, de hat emberek vagyunk, nem gepek. Ez eddig is elhangzott mar parszor.
2. elmelet: Probalj elvontabban gondolkozni, esetleg olvass vissza. Es probald az erdot is eszrevenni a fa mogott.
2. elmelet: Probalj elvontabban gondolkozni, esetleg olvass vissza. Es probald az erdot is eszrevenni a fa mogott.
bela2 2008.05.11. 23:50:30
Na jo, meggyoztel! :-)
Tenyleg rossz a bias-os gondolkodas, ha az ember az eloiteletei rabja marad miatta. Es sajnos ilyenre sok pelda van...
Tenyleg rossz a bias-os gondolkodas, ha az ember az eloiteletei rabja marad miatta. Es sajnos ilyenre sok pelda van...
nyari mikulas (törölt) 2008.05.12. 00:10:44
Bela: "Az elmeletben vegtelen szamu fekete es feher pont van. Ez igy van a peldaban is, vegtelen szamu jo es rossz szamharmas letezik."
Igazad van abban az esetben ha nem szabalyt keresunk, hanem csak peldakat (pontokat).
Egy hipotezist egytelen (vagy nehany) cafolat utan el lehet vetni, nem szukseges tovabbi teszteket vegezni. A szamos peldaban ha tesztelted a 2,2,2 es az 5,5,5 szamokat, es tagado valaszt kaptal, akkor nem celszeru a 3,3,3, a 4,4,4 a 6,6,6 stb harmasok tesztelese, pedig vegtelen sok ilyen letezik.
A terkep pontjai nem ilyenek, ott mindegyiket egyenkent meg kell vizsgalni, ha nem szabalyos alakzatot keresunk, hanem csak azt, hogy melyik pont fekete, melyik feher.
Nem tudom erheto-e a kulonbseg, vagy probaljam jobban kifejteni?
Igazad van abban az esetben ha nem szabalyt keresunk, hanem csak peldakat (pontokat).
Egy hipotezist egytelen (vagy nehany) cafolat utan el lehet vetni, nem szukseges tovabbi teszteket vegezni. A szamos peldaban ha tesztelted a 2,2,2 es az 5,5,5 szamokat, es tagado valaszt kaptal, akkor nem celszeru a 3,3,3, a 4,4,4 a 6,6,6 stb harmasok tesztelese, pedig vegtelen sok ilyen letezik.
A terkep pontjai nem ilyenek, ott mindegyiket egyenkent meg kell vizsgalni, ha nem szabalyos alakzatot keresunk, hanem csak azt, hogy melyik pont fekete, melyik feher.
Nem tudom erheto-e a kulonbseg, vagy probaljam jobban kifejteni?
nyari mikulas (törölt) 2008.05.12. 00:29:14
hvuk:
"1. Nem értem miért volt szükséges mind az eredeti, mind András kísérletében induló számhármast definiálni."
Epp azert, mert ez a szamharmas minden iskolat vegzett ember gondolkodasat egy megahatarozott (teves) iranyba inditja. Ez a szep a feladatban.
2. "András azt állítja, hogy a szabálytól nem függ az optimális pozitív-negatív arány, az mindig 50%"
Megallapodtunk benne, hogy nem az. Andras szavait idezem: "Fölösleges azon lovagolni, hogy 50% vagy 40 vagy 70 az optimum, ez nem ennyire egzakt dolog, más tényezőktől is függ. Van egy korreláció, ennyi. Magasabb próbaszám mellett kisebb arány is elég."
6."Mi lenne vajon a végkifejlete egy olyan kísérletnek, ahol a szabály az, hogy a számhármas vagy a 2, 4, 6 vagy pedig csupa negatív számból áll? Van egy olyan sejtésem, hogy egy szemernyi confirmation bias nem lépne fel, a tesztelt számhármasok döntő többsége nem felelne meg a szabálynak."
Egyetertek abban, hogy a kiserlet kezdeten sokkal tobb negativ valaszt varok en is.
Ugyanakkor a megerositesi tevedes itt is fellepne, ha valaki felismeri, hogy a pozitiv szamok kozul csak a 2,4,6 felel meg, van eselye annak, megallna itt, es nem vizsgalna a negativ szamokat.
Fenntartom, amit tobbszor kifejtettem, hogy a confirmation bias az nem a kapott negativ valaszok szama, hanem azoknak a kerdeseknek a kerulese, amelyekre tagado valaszt varunk. A confirmation bias az en olvasatomban azoknak a kerdeseknek az aranya, amelyekre helyeslo illetve amelyekre tagado valaszt varunk, fuggetlenul attol, hogy milyen valaszt kapunk.
"1. Nem értem miért volt szükséges mind az eredeti, mind András kísérletében induló számhármast definiálni."
Epp azert, mert ez a szamharmas minden iskolat vegzett ember gondolkodasat egy megahatarozott (teves) iranyba inditja. Ez a szep a feladatban.
2. "András azt állítja, hogy a szabálytól nem függ az optimális pozitív-negatív arány, az mindig 50%"
Megallapodtunk benne, hogy nem az. Andras szavait idezem: "Fölösleges azon lovagolni, hogy 50% vagy 40 vagy 70 az optimum, ez nem ennyire egzakt dolog, más tényezőktől is függ. Van egy korreláció, ennyi. Magasabb próbaszám mellett kisebb arány is elég."
6."Mi lenne vajon a végkifejlete egy olyan kísérletnek, ahol a szabály az, hogy a számhármas vagy a 2, 4, 6 vagy pedig csupa negatív számból áll? Van egy olyan sejtésem, hogy egy szemernyi confirmation bias nem lépne fel, a tesztelt számhármasok döntő többsége nem felelne meg a szabálynak."
Egyetertek abban, hogy a kiserlet kezdeten sokkal tobb negativ valaszt varok en is.
Ugyanakkor a megerositesi tevedes itt is fellepne, ha valaki felismeri, hogy a pozitiv szamok kozul csak a 2,4,6 felel meg, van eselye annak, megallna itt, es nem vizsgalna a negativ szamokat.
Fenntartom, amit tobbszor kifejtettem, hogy a confirmation bias az nem a kapott negativ valaszok szama, hanem azoknak a kerdeseknek a kerulese, amelyekre tagado valaszt varunk. A confirmation bias az en olvasatomban azoknak a kerdeseknek az aranya, amelyekre helyeslo illetve amelyekre tagado valaszt varunk, fuggetlenul attol, hogy milyen valaszt kapunk.
hvuk 2008.05.12. 00:39:41
"1. strategia: Es ki mondta, hogy rossz a bias-os gondolkodas? Nyilvan elmeletileg nem korrekt, de hat emberek vagyunk, nem gepek. Ez eddig is elhangzott mar parszor."
Persze, ezt senki nem mondta. De én negatív felhangot éreztem kicsendűlni belőle. :)
Amúgy meg szerintem elvárható lenne, ha egy ilyen kísérlet előtt leírnák (értsd: bizonyítanák), hogy mi az optimális pozitív/negatív kísérlet arány. Ebben a kíséreltben ez meg sem volt kísérelve.
"2. elmelet: Probalj elvontabban gondolkozni, esetleg olvass vissza. Es probald az erdot is eszrevenni a fa mogott."
Én az összes hozzászólást elolvastam ebben a topicban, mivel ugye én kezdtem ezt az egész vitát. Elvontnak meg pont elég elvont a gondolkodásom. Viszont még mindig várom, hogy megnevezd azt az elméletet ami alapján 50% az optimális arány ebben a kísérletben. Persze a "csak" is válasz, ne habozd azt beírni, ha tényleg az az indokod! :)
Persze, ezt senki nem mondta. De én negatív felhangot éreztem kicsendűlni belőle. :)
Amúgy meg szerintem elvárható lenne, ha egy ilyen kísérlet előtt leírnák (értsd: bizonyítanák), hogy mi az optimális pozitív/negatív kísérlet arány. Ebben a kíséreltben ez meg sem volt kísérelve.
"2. elmelet: Probalj elvontabban gondolkozni, esetleg olvass vissza. Es probald az erdot is eszrevenni a fa mogott."
Én az összes hozzászólást elolvastam ebben a topicban, mivel ugye én kezdtem ezt az egész vitát. Elvontnak meg pont elég elvont a gondolkodásom. Viszont még mindig várom, hogy megnevezd azt az elméletet ami alapján 50% az optimális arány ebben a kísérletben. Persze a "csak" is válasz, ne habozd azt beírni, ha tényleg az az indokod! :)
hvuk 2008.05.12. 00:40:59
Tamas55!
"Epp azert, mert ez a szamharmas minden iskolat vegzett ember gondolkodasat egy megahatarozott (teves) iranyba inditja. Ez a szep a feladatban."
Ez szép, meg minden, de szerintem mind a confirmation bias létezésére, mind annak nagyságára korrektebb eredményt kaptunk volna egy kevésbé manupilatív feladatra.
"Epp azert, mert ez a szamharmas minden iskolat vegzett ember gondolkodasat egy megahatarozott (teves) iranyba inditja. Ez a szep a feladatban."
Ez szép, meg minden, de szerintem mind a confirmation bias létezésére, mind annak nagyságára korrektebb eredményt kaptunk volna egy kevésbé manupilatív feladatra.
nyari mikulas (törölt) 2008.05.12. 01:01:00
Ha a confirmation biast ugy ertelmezed, mint az elobb en, akkor mindegy mi a feladat.
Ebben az feladatban az a szep, hogy itt a confirmation bias nagy esellyel eredmenyez hibas megoldast, igy nagyobb a demonstrativ ereje.
Ebben az feladatban az a szep, hogy itt a confirmation bias nagy esellyel eredmenyez hibas megoldast, igy nagyobb a demonstrativ ereje.
bela2 2008.05.12. 11:04:03
hvuk, lasd 2008.05.11. 00:01:21 es kornyeki megjegyzeseim a terkepfelderitesrol. Szerintem pedig eppen azert kezdted a vitat, mert nem tudsz elvonatkoztatni az adott peldatol.
tamas, attol, ha a 2,2,2 nem jo es az 5,5,5 sem jo, nem tudhatod, hogy a 3,3,3 jo-e. Termeszetesen egy ilyen feladatban lehetetlen vegtelen szamu pontot tesztelni, igy biztosan nem lehet pontosan korbejarni a szabalyt. Eppen errol beszelek, minel tobb kiserletet vegez valaki, lehetoleg minel kiegyensulyozottabb eredmenyeloszlassal, annal pontosabban tud tippelni a szabalyra. Persze nem tudhatja, hogy a 678326587648725657823658248 feletti szamoknal nincs-e valami valtozas...
Komolyan kerlek titeket, ne csak a 2+2=4 szintu szabalyokra gondoljatok! Free your mind!
A hetkoznapi eletben felmerulo problemak egy picike halmazat vagy vetuletet adjak a matematikanak. Ezek a vetuletek persze torzulhatnak is, de az alapveto iranyvonalak nem modosulnak.
Ebben a kerdeskorben erdekesen keveredik a matematika, a statisztika es a pszichologia. Nem lehet csak az egyik menten velemenyt mondani az egeszrol.
tamas, attol, ha a 2,2,2 nem jo es az 5,5,5 sem jo, nem tudhatod, hogy a 3,3,3 jo-e. Termeszetesen egy ilyen feladatban lehetetlen vegtelen szamu pontot tesztelni, igy biztosan nem lehet pontosan korbejarni a szabalyt. Eppen errol beszelek, minel tobb kiserletet vegez valaki, lehetoleg minel kiegyensulyozottabb eredmenyeloszlassal, annal pontosabban tud tippelni a szabalyra. Persze nem tudhatja, hogy a 678326587648725657823658248 feletti szamoknal nincs-e valami valtozas...
Komolyan kerlek titeket, ne csak a 2+2=4 szintu szabalyokra gondoljatok! Free your mind!
A hetkoznapi eletben felmerulo problemak egy picike halmazat vagy vetuletet adjak a matematikanak. Ezek a vetuletek persze torzulhatnak is, de az alapveto iranyvonalak nem modosulnak.
Ebben a kerdeskorben erdekesen keveredik a matematika, a statisztika es a pszichologia. Nem lehet csak az egyik menten velemenyt mondani az egeszrol.
nyari mikulas (törölt) 2008.05.12. 13:42:30
Bela2, kenytelenek vagyunk a szabalyokra es a peldara gondolni, mert arrol beszelgetunk.
Ha Te altalaban filozofiai szinten vagy a hetkoznapi elet szintjan akarsz a megerositesi tevdesrol beszelgetni, es benne vagyok, javaslom, hogy nyiss neki egy uj topikot a forumon. www.szkeptikustarsasag.hu/forum
A pelda eseten igazad van, hogy a 3,3,3 akar jo is lehet, es minden szamharmast meg kell vizsgalni ahhoz, hogy biztos legyel benne, nincs-e valahol egy kiegeszitese a szabalynak, amelyik azt a kivetelt megengedi, vagy tiltja. Ebben az esetben, ha szisztematikusan az osszes harmast vizsgalod, a ebben a konkret feladatban 1/6 lesz a megerosito es 5/6 a cafolo valaszok aranya.
Abban a feladatban meg, ahol a megoldas az, hogy legalalbb egy paros szam kell legyen a harmasban ha jol szamolom, akkor 1/8 lesz a cafolo es 7/8 a megerosito valszok aranya.
Tehat ha a Te logikadat kovetjuk, akkor is a feladattol fugg a cafolo es a megerosito valaszok szama akkor is, ha semmi confirmation bias nincsen, mert teljesen vakon, sorra vizsgaljuk az osszes lehetseges szamharmast.
Ennyit a matamatikai oldalarol a feladatnak.
Miutan megvizsgaltam a feladatot a Te logikad szerint is, legyen szabad megjegyeznem, hogy sem a matematikaban, sem a hetkoznapi problemamegoldas soran nem azt a megkozelitest hasznaljuk.
Itt is es ott is szabalyokat keresunk, mert az sokkal hatekonyabb, sokkal kevesebb kiserletbol eljutunk a helyes, vagy he nem is helyes, de hasznalhato megoldashoz.
Itt jon be a confirmation bias, hogy miutan megsejtunk egy szabalyt, utana olyan eseteket vizsgalunk, amelyek megfelelnek a szabalynak, es nem teszteljuk azokat, amelyektol cafolo valaszt varunk.
Vegul is ez nem egy rossz strategia sok esetben!
Ha valaki a fenti peldaban megvizsgalja a 2,4,6,8,10 sort, megerositest kap, es elkonyveli, hogy a szabaly kettesevel novekvo paros szamok, akkor ezzel a szaballyal vegtelenul sok helyes megoldast tud generalni, es sosem fog hibat kapni. Valamilyen szinten jo szabaly ez is. Csak nem teljes.
Korulbelul olyan, mint a hetkoznapi eletben az ember koszal a termeszetben es felismeri, hogy a piros szinu puha bogyok finomak es taplaloak. Akkortol csak piros szinu bogyokat keres es csak azokat eszi, es nem fecserli az energiajat zold szinu, a barna szinu kemeny bogyok kostolgatasara. Elso kozlitesben jo strategiat valsztott, tobb ennivalot fog talalni, mint az aki szintematikusan mindent (kavicsot, homokot, fatorzseket, kakit, fuvet vegigkostol, mert hatha van azok kozott is eheto, meg akkor is, ha az eddig kostoltakba beletort a foga.
De ez mar nagyon filozofia es lehet, hogy Andras ilyen iranyu posztot keszit elo, ne vegyuk el tole.
Ha Te altalaban filozofiai szinten vagy a hetkoznapi elet szintjan akarsz a megerositesi tevdesrol beszelgetni, es benne vagyok, javaslom, hogy nyiss neki egy uj topikot a forumon. www.szkeptikustarsasag.hu/forum
A pelda eseten igazad van, hogy a 3,3,3 akar jo is lehet, es minden szamharmast meg kell vizsgalni ahhoz, hogy biztos legyel benne, nincs-e valahol egy kiegeszitese a szabalynak, amelyik azt a kivetelt megengedi, vagy tiltja. Ebben az esetben, ha szisztematikusan az osszes harmast vizsgalod, a ebben a konkret feladatban 1/6 lesz a megerosito es 5/6 a cafolo valaszok aranya.
Abban a feladatban meg, ahol a megoldas az, hogy legalalbb egy paros szam kell legyen a harmasban ha jol szamolom, akkor 1/8 lesz a cafolo es 7/8 a megerosito valszok aranya.
Tehat ha a Te logikadat kovetjuk, akkor is a feladattol fugg a cafolo es a megerosito valaszok szama akkor is, ha semmi confirmation bias nincsen, mert teljesen vakon, sorra vizsgaljuk az osszes lehetseges szamharmast.
Ennyit a matamatikai oldalarol a feladatnak.
Miutan megvizsgaltam a feladatot a Te logikad szerint is, legyen szabad megjegyeznem, hogy sem a matematikaban, sem a hetkoznapi problemamegoldas soran nem azt a megkozelitest hasznaljuk.
Itt is es ott is szabalyokat keresunk, mert az sokkal hatekonyabb, sokkal kevesebb kiserletbol eljutunk a helyes, vagy he nem is helyes, de hasznalhato megoldashoz.
Itt jon be a confirmation bias, hogy miutan megsejtunk egy szabalyt, utana olyan eseteket vizsgalunk, amelyek megfelelnek a szabalynak, es nem teszteljuk azokat, amelyektol cafolo valaszt varunk.
Vegul is ez nem egy rossz strategia sok esetben!
Ha valaki a fenti peldaban megvizsgalja a 2,4,6,8,10 sort, megerositest kap, es elkonyveli, hogy a szabaly kettesevel novekvo paros szamok, akkor ezzel a szaballyal vegtelenul sok helyes megoldast tud generalni, es sosem fog hibat kapni. Valamilyen szinten jo szabaly ez is. Csak nem teljes.
Korulbelul olyan, mint a hetkoznapi eletben az ember koszal a termeszetben es felismeri, hogy a piros szinu puha bogyok finomak es taplaloak. Akkortol csak piros szinu bogyokat keres es csak azokat eszi, es nem fecserli az energiajat zold szinu, a barna szinu kemeny bogyok kostolgatasara. Elso kozlitesben jo strategiat valsztott, tobb ennivalot fog talalni, mint az aki szintematikusan mindent (kavicsot, homokot, fatorzseket, kakit, fuvet vegigkostol, mert hatha van azok kozott is eheto, meg akkor is, ha az eddig kostoltakba beletort a foga.
De ez mar nagyon filozofia es lehet, hogy Andras ilyen iranyu posztot keszit elo, ne vegyuk el tole.
bela2 2008.05.12. 16:33:18
Egyetertek. Remekul leirtad a confirmation biast. Errol beszeltem en is. Itt nincs vita kozottunk.
A 3,3,3-mal kapcsolatban van egy pici, nem szisztematikusan az osszes pontot kell tesztelni, hanem minel tobb, lehetoleg vegtelen szamu szabalyt. Amig csak megerositest kapsz, mindig bovitheted a szabalyod ervenyesseget, hogy tudd, meddig er. Amig kello szamu cafolat be nem hatarolja.
Azzal is egyetertek, hogy egyunk piros bogyot, mert "Jart utat a jaratlanert...", ez a biztonsagi megoldas, egy eletunk van. De mi van, ha elfogy? Vagy van helyette jobb, taplalobb? Valakinek fel kell aldoznia magat a tudomanyert :-)
A 3,3,3-mal kapcsolatban van egy pici, nem szisztematikusan az osszes pontot kell tesztelni, hanem minel tobb, lehetoleg vegtelen szamu szabalyt. Amig csak megerositest kapsz, mindig bovitheted a szabalyod ervenyesseget, hogy tudd, meddig er. Amig kello szamu cafolat be nem hatarolja.
Azzal is egyetertek, hogy egyunk piros bogyot, mert "Jart utat a jaratlanert...", ez a biztonsagi megoldas, egy eletunk van. De mi van, ha elfogy? Vagy van helyette jobb, taplalobb? Valakinek fel kell aldoznia magat a tudomanyert :-)
wice 2008.05.13. 10:48:07
szerintem megallapodhatunk abban (es talan Andras se fog ezzel vitatkozni), h
1. ha vkinek confirmation biasa van, akkor tobb, mint valoszinu, h tobb "megfelelt", mint "nem felelt meg" valasz utan fogja megadni a megoldasat, de
2. ha valaki tobb "megfelelt", mint "nem felelt meg" valasz utan adta meg a megoldasat, abbol meg nem kovetkezik szuksegszeruen, h confirmation biasa van.
ha jol sejtem, mi pusztan ennyit szeretnenk elfogadtatni Andrassal, mert vmiert ugy tunik, mintha ezt vitatna, kozben meg lehet, h nem is.
1. ha vkinek confirmation biasa van, akkor tobb, mint valoszinu, h tobb "megfelelt", mint "nem felelt meg" valasz utan fogja megadni a megoldasat, de
2. ha valaki tobb "megfelelt", mint "nem felelt meg" valasz utan adta meg a megoldasat, abbol meg nem kovetkezik szuksegszeruen, h confirmation biasa van.
ha jol sejtem, mi pusztan ennyit szeretnenk elfogadtatni Andrassal, mert vmiert ugy tunik, mintha ezt vitatna, kozben meg lehet, h nem is.
bela2 2008.05.14. 09:51:08
Hu, ez ovon aluli volt...
"Tisztelt rendorseg, higgyek el, nekem nincs gyorshajtasom, csak ugye erre a szakaszra nem szokas sebessegkorlatozast kitenni."
"Tisztelt rendorseg, higgyek el, nekem nincs gyorshajtasom, csak ugye erre a szakaszra nem szokas sebessegkorlatozast kitenni."
Nádori Gergely 2008.05.29. 09:39:59
Ez a kártyajátk:
en.wikipedia.org/wiki/Eleusis_(game)
szintén remekül szemlélteti a tudományos módszert, én szoktam is játszani diákjaimmal.
en.wikipedia.org/wiki/Eleusis_(game)
szintén remekül szemlélteti a tudományos módszert, én szoktam is játszani diákjaimmal.






Az utolsó 100 komment: